ΧβΡΩΡΎ»ί
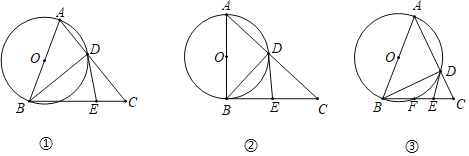
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎRtΓςABC÷–Θ§ΓœBACΘΫ90ΓψΘ§ABΘΫ6Θ§ACΘΫ8Θ§ΒψDΘ§EΘ§NΖ÷±π «ΓςABCΒΡABΘ§ACΘ§BC±Ώ…œΒΡ÷–ΒψΘ§Ν§Ϋ”ANΘ§DEΫΜ”ΎΒψMΘ°
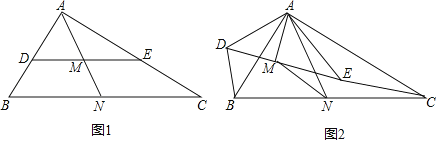
Θ®1Θ©Ιέ≤λ≤¬œκΘΚ![]() ΒΡ÷ΒΈΣΓΓ ΓΓΘΚ
ΒΡ÷ΒΈΣΓΓ ΓΓΘΚ![]() ΒΡ÷ΒΈΣΓΓ ΓΓΘΜ
ΒΡ÷ΒΈΣΓΓ ΓΓΘΜ
Θ®2Θ©ΧΫΨΩ”κ÷ΛΟςΘΚΫΪΓςADE»ΤΒψAΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣΠΝΫ«Θ®0ΓψΘΦΠΝΘΦ360ΓψΘ©Θ§«“ΓςADEΡΎ≤ΩΒΡœΏΕΈAMΥφ÷°–ΐΉΣΘ§»γΆΦ2Υυ ΨΘ§Ν§Ϋ”BDΘ§CEΘ§MNΘ§ ‘ΧΫΨΩœΏΕΈBD”κCEΚΆBD”κMN÷°ΦδΖ÷±π”– ≤Ο¥―υΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΘΜ
Θ®3Θ©ΆΊ’Ι”κ―”…λΘΚΓςADE‘Ύ–ΐΉΣΒΡΙΐ≥Χ÷–Θ§…η÷±œΏCE”κBDœύΫΜ”ΎΒψFΘ§Β±ΓœCAEΘΫ90Γψ ±Θ§BFΘΫΓΓ ΓΓΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Θ§
Θ§![]() Θ§ΦϊΫβΈωΘΜΘ®3Θ©
Θ§ΦϊΫβΈωΘΜΘ®3Θ©![]() Μρ
Μρ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΩ…ΒΟAD=BD=3Θ§AE=EC=4Θ§DEΓΈBCΘ§”…Ι¥Ι…Ε®άμΩ…«σBC=10Θ§”…÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟAN=5Θ§”…ΤΫ––œΏΖ÷œΏΕΈ≥…±»άΐΩ…ΒΟ![]() Θ§Φ¥Ω…«σΫβΘΜ
Θ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©”…–ΐΉΣΒΡ–‘÷ Ω…÷ΛΓςADBΓΉΓςAECΘ§ΓςABDΓΉΓςANMΘ§”…œύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…«σΫβΘΜ
Θ®3Θ©Ζ÷Β±ΒψE‘ΎœΏΕΈAB…œΚΆΒψE‘ΎœΏΕΈBAΒΡ―”≥ΛœΏ…œ‘ΎΝΫ÷÷«ιΩωΧ÷¬έΘ§”…Ι¥Ι…Ε®άμΩ…«σBDΘ§CEΒΡ≥ΛΘ§”…œύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…«σBFΒΡ≥ΛΘ°
Θ®1Θ©ΓΏAB=6Θ§AC=8Θ§ΒψDΘ§EΖ÷±π «ΓςABCΒΡABΘ§AC±Ώ…œΒΡ÷–ΒψΘ§ΓύAD=BD=3Θ§AE=EC=4Θ§DEΓΈBCΘ§Γύ![]() Θ°
Θ°
ΓΏΓœBAC=90ΓψΘ§AB=6Θ§AC=8Θ§ΓύBC![]() 10Θ°
10Θ°
ΓΏΒψN «BC…œΒΡ÷–ΒψΘ§ΓύAN![]() BC=5Θ°
BC=5Θ°
ΓΏDEΓΈBCΘ§Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©![]() Θ§
Θ§![]() Θ°άμ”…»γœ¬ΘΚ
Θ°άμ”…»γœ¬ΘΚ
”…ΆΦ1Ω…ΒΟΘΚΓΏDEΓΈBCΘ§ΓύΓςADEΓΉΓςABCΘ§ΓςADMΓΉΓςABMΘ§Γύ![]() Θ§
Θ§![]() Θ°
Θ°
ΓΏΫΪΓςADE»ΤΒψAΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣΠΝΫ«Θ§ΓύΓœDAB=ΓœCAE=ΠΝΘ§«“![]() Θ§ΓύΓςADBΓΉΓςAECΘ§Γύ
Θ§ΓύΓςADBΓΉΓςAECΘ§Γύ![]() Θ°
Θ°
ΓΏΓœBAD=ΓœMAN=ΠΝΘ§«“![]() Θ§ΓύΓςABDΓΉΓςANMΘ§Γύ
Θ§ΓύΓςABDΓΉΓςANMΘ§Γύ![]() Θ°
Θ°
Θ®3Θ©»γΆΦΘ§Β±ΒψE‘ΎœΏΕΈAB…œ ±Θ°
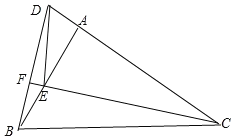
ΓΏAB=6Θ§AC=8Θ§AE=4Θ§AD=3Θ§ΓύCD=11Θ§BD![]() 3
3![]() Θ§CE
Θ§CE![]() 4
4![]() Θ°
Θ°
ΓΏ![]() Θ§Γύ
Θ§Γύ![]() Θ§«“ΓœDAE=ΓœEAC=90ΓψΘ§ΓύΓςAECΓΉΓςADBΘ§ΓύΓœABD=ΓœACEΘ§«“ΓœABD+ΓœBDA=90ΓψΘ§ΓύΓœACE+ΓœBDA=90ΓψΘ§ΓύΓœDFC=90Γψ=ΓœBACΘ§«“ΓœACE=ΓœACEΘ§ΓύΓςACEΓΉΓςFCDΘ§Γύ
Θ§«“ΓœDAE=ΓœEAC=90ΓψΘ§ΓύΓςAECΓΉΓςADBΘ§ΓύΓœABD=ΓœACEΘ§«“ΓœABD+ΓœBDA=90ΓψΘ§ΓύΓœACE+ΓœBDA=90ΓψΘ§ΓύΓœDFC=90Γψ=ΓœBACΘ§«“ΓœACE=ΓœACEΘ§ΓύΓςACEΓΉΓςFCDΘ§Γύ![]() Θ§ΓύDF
Θ§ΓύDF![]() Θ§ΓύBF=BD©¹DF
Θ§ΓύBF=BD©¹DF![]() Θ°
Θ°
»γΆΦΘ§Β±ΒψE‘ΎœΏΕΈBAΒΡ―”≥ΛœΏ…œΘ°

Ά§άμΩ…ΒΟΘΚBD=3![]() Θ§BE=10Θ§ΓœBAC=ΓœEFB=90ΓψΘ°
Θ§BE=10Θ§ΓœBAC=ΓœEFB=90ΓψΘ°
ΓΏΓœEBF=ΓœEBFΘ§ΓœBAD=ΓœEFB=90ΓψΘ§ΓύΓςADBΓΉΓςFEBΘ§Γύ![]() Θ§ΓύBF
Θ§ΓύBF![]() 4
4![]() Θ°
Θ°
Ήέ…œΥυ ωΘΚΒ±ΓœCAE=90Γψ ±Θ§BF=4![]() Μρ
Μρ![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ4![]() Μρ
Μρ![]() Θ°
Θ°

ΓΨΧβΡΩΓΩΫϋ»’Θ§»Ϊ ΓΗςΒΊ –ΒΡ2019Ρξ≥θ÷–±œ“Β…ΐ―ßΧε”ΐΩΦ ‘ΙΛΉς’ΐ“ά’’Ρ≥ ΓΫΧ”ΐΧϋΒΡΨΏΧε“Σ«σ‘Ύ”–Χθ≤ΜΈ…ΒΡΫχ––Β±÷–Θ§Ρ≥÷–―ß‘Ύ’ΐ ΫΩΦ ‘«ΑΘ§ΈΣΝΥ»ΟΆ§―ßΟ«‘Ύ÷–’–Χε”ΐΩΦ ‘÷–ΜώΒΟάμœκ≥…Φ®Θ§Ά§ ±ΈΣΝΥΝΥΫβ―ß…ζΒΡΒ±«ΑΥ°ΤΫΘ§Α¥≈ζ¥ΈΫχ––ΝΥΡΘΡβΩΦ ‘Θ§≤ΔΥφΜζ≥ι»Γ»τΗ…Οϊ―ß…ζΈ ΨμΒς≤ιΘ§œ÷ΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γœ¬≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ±μΘΚ
Ήι±π | ≥…Φ®ΖΕΈßxΘ®Ζ÷Θ© | ΤΒ ΐΘ®»Υ ΐΘ© |
A | 60ΘΦxΓή70 | 54 |
B | 50ΘΦxΓή60 | m |
C | 40ΘΦxΓή50 | n |
D | 30ΘΦxΓή40 | 6 |
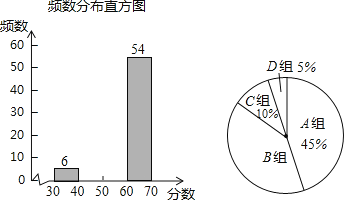
Θ®1Θ©’β¥ΈΒς≤ιΒΡΉή»Υ ΐ”–ΓΓ ΓΓ»ΥΘ§±μ÷–ΒΡmΘΫΓΓ ΓΓΘ§nΘΫΓΓ ΓΓΘΜ
Θ®2Θ©…»–ΈΆ≥ΦΤΆΦ÷–BΉιΕ‘”ΠΒΡ‘≤–ΡΫ«ΈΣΓΓ ΓΓΓψΘΜ
Θ®3Θ©«κ≤Ι»ΪΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΜ
Θ®4Θ©»τΗΟ–ΘΨ≈ΡξΦΕΙ≤”–―ß…ζ2700ΟϊΘ§«“ΕΦ≤ΈΦ”ΝΥ’ΐ ΫΒΡ≥θ÷–±œ“Β…ΐ―ßΧε”ΐΩΦ ‘Θ§–ΓΜΣ“≤≤ΈΦ”ΝΥ’β¥ΈΩΦ ‘≤ΔΒΟΝΥ67Ζ÷Θ§»τΙφΕ®60Ζ÷“‘…œΈΣ”≈–ψΘ§Χε”ΐάœ Πœκ“Σ‘ΎΜώΒΟ”≈–ψΒΡ―ß…ζ÷–ΥφΜζ≥ι≥ω1ΟϊΘ§ΉςΈΣ―ß…ζ¥ζ±μœρ―ßΒή―ßΟΟΟ«¥Ϊ ΎΨ≠―ιΘ§«σ≥ιΒΫ–ΓΜΣΒΡΗ≈¬ Θ°