��Ŀ����
����Ŀ������һ���ڼ�������̳������������̳��ķ����ǣ���һ���������������4����ȫ��ͬ��С�����Ϸֱ�ꡰ0Ԫ����20Ԫ����30Ԫ����50Ԫ�����˿�ÿ������300Ԫ�Ϳɴ������ﲻ�Żص�����2����������С��������֮�Ϳɻ���Ӧ�۸����Ʒ�����̳��ķ����ǣ���һ���������������2����ȫ��ͬ��С�����Ϸֱ�ꡰ5Ԫ����30Ԫ�����˿�ÿ������100Ԫ���Ϳɴ��������зŻص�����1������С��������ɻ���Ӧ�۸����Ʒ.ij�˿�������300Ԫ.
(1)���û���״ͼ���б���������ù˿��ڼ��̳������Ʒ���ܼ�ֵ������50Ԫ�ĸ��ʣ�
(2)�жϸù˿�ȥ�ĸ��̳�����ʹ�����Ʒ���ܼ�ֵ������50Ԫ�������˵������.
���𰸡�(1)![]() ��(2)�����̳����ѣ����ɼ�����.
��(2)�����̳����ѣ����ɼ�����.
��������
��1�����ȸ��������г�����Ȼ���ɱ���������еȿ��ܵĽ����ù˿��ڼ��̳�������Ʒ�Ľ�����50Ԫ������������ø��ʹ�ʽ��⼴����ô�
��2��������״ͼ����˿�ȥ���̳����ѻ����Ʒ���ܼ�ֵ������50Ԫ�ĸ��ʣ��Ƚϼ����̳����ʼ��ɽ���
(1)�ڼ��̳�����
0 | 20 | 30 | 50 | |
0 | 20 | 30 | 50 | |
20 | 20 | 50 | 70 | |
30 | 30 | 50 | 80 | |
50 | 50 | 70 | 80 |
P(�ײ�����50Ԫ)=![]()
(2)�����̳����ѣ�
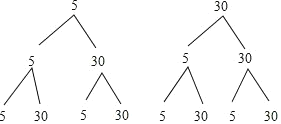
�� 15 40 40 65 40 65 65 90
P(�Ҳ�����50Ԫ)=![]()
P(�ײ�����50Ԫ)>P(�Ҳ�����50Ԫ)
���ù˿�ȥ���̳����ѣ������Ʒ���ܼ�ֵ������50Ԫ�ĸ��ʴ�

 ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�����Ŀ��ijˮ������10Ԫ/ǧ�˵ļ۸�ij��ˮ���������ۣ������г������ò����������±���
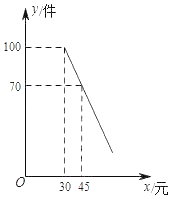
���ۼ۸�x��Ԫ/ǧ�ˣ� | 10 | 13 | 16 | 19 | 22 |
��������y��ǧ�ˣ� | 100 | 85 | 70 | 55 | 40 |
��1������ݱ��е����ݣ�����ѧ����һ�κ��������κ�����������������֪ʶ�̻�y��x֮��ĺ�����ϵ��
��2����ˮ����Ӧ�����ȷ������ˮ�������ۼ۸���ʹ�������������
��3������ˮ����ƽ��ÿ����1ǧ������ˮ�������aǧ�ˣ���20��x��22ʱ��ˮ�����ջ��������ֵΪ405Ԫ����a��ֵ��
����Ŀ��ij��λ��Ҫ��֯���г�����������Ա�������ù�����Ʊ�۸����£�
��Ʊ���� | 1��50 | 51��100 | 100���� |
��Ʊ�۸� | 13Ԫ/�� | 11Ԫ/�� | 9Ԫ/�� |
�����������Ϊ���壬ѡ��������ͬ��ʱ��ֱ�Ʊ������������֧����Ʊ��Ϊ1245Ԫ������������ź���һ����Ϊһ�����壬ͬһʱ�乺Ʊ������������֧����Ʊ��Ϊ945Ԫ����ô�ù�˾��������������֮��ľ���ֵΪ_____��