Question

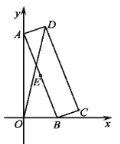
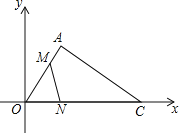
【题目】如图，点O是平面直角坐标系的原点，点A（，3），AC⊥OA与x轴的交点为C．动点M以每秒个单位长度由点A向点O运动．同时，动点N以每秒3个单位长度由点O向点C运动，当一动点先到终点时，另一动点立即停止运动．

（1）写出∠AOC的值；

（2）用t表示出四边形AMNC的面积；

（3）求点P的坐标，使得以O、N、M、P为顶点的四边形是特殊的平行四边形？

Answer 1

【答案】（1）30°；（2）；（3）.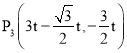

【解析】

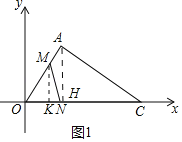
（1）如图1中，作AH⊥OC于H．在Rt△AOH中，解直角三角形求出∠AOH即可解决问题．

（2）作MK⊥BC于K．根据S四边形AMNC＝S△OAC﹣S△OMN，计算即可．

（3）分别考虑以OM，ON，MN为平行四边形的对角线，利用平行四边形的性质求解即可．

解：（1）如图1中，作AH⊥OC于H．

∵A（，3），

∴OH＝，AH＝3，

∴tan∠AOH＝＝，

∴∠AOH＝60°，

∵OA⊥AC，

∴∠OAC＝90°，

∴∠ACO＝30°．

（2）作MK⊥BC于K．

在Rt△AOH中，∵OH＝，∠OAH＝30°，

∴OA＝2OH＝2，

在Rt△AOC中，∵∠AOC＝30°，OA＝2，

∴AC＝OA＝6，

∵OM＝t，

∴MK＝OMsin60°＝t，

∴S四边形AMNC＝S△OAC﹣S△OMN

＝OAAC﹣ONMKa

＝×2×6﹣×3t×t

＝6﹣t2（0＜t＜2）．

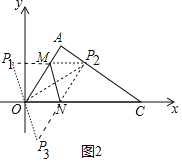
（3）当四边形CNMP1是平行四边形时，P1（t﹣3t，t）．

当四边形ONP2M是平行四边形时，P2（t+3t，t）．

当四边形OMNP3是平行四边形时，P3（3t﹣t，﹣t）．