题目内容
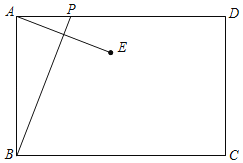
【题目】如图,矩形硬纸片ABCD的顶点A在![]() 轴的正半轴及原点上滑动,顶点B在
轴的正半轴及原点上滑动,顶点B在![]() 轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为
轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为![]() ,其中正确的结论是_________(填写序号).
,其中正确的结论是_________(填写序号).
【答案】②③
【解析】
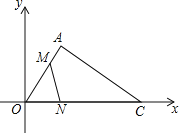
①由条件可知AB=24,则AB的中点E的运动轨迹是圆弧,最后根据弧长公式即可计算出点E所经过的路径长;②当△OAB的面积最大时,因为AB=24,所以△OAB为等腰直角三角形,即OA=OB,可求出最大面积为144;③当O、E、D三点共线时,OD最大,过点D作DF⊥y轴于点F,可求出OD=25,证明△DFA∽△AOB和△DFO∽△BOA,可求出DF长,则D点坐标可求出.
解:∵点E为AB的中点,AB=24,
![]()
∴AB的中点E的运动轨迹是以点O为圆心,12为半径的一段圆弧,
∵∠AOB=90°,
∴点E经过的路径长为![]() ,故①错误;
,故①错误;
当△OAB的面积最大时,因为AB=24,所以△OAB为等腰直角三角形,即OA=OB,
∵E为AB的中点,
![]()
![]() ,故②正确;
,故②正确;
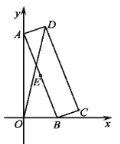
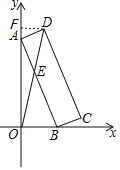
如图,当O、E、D三点共线时,OD最大,过点D作DF⊥y轴于点F,
![]()
![]()
∴OD=DE+OE=13+12=25,
设DF=x,
![]()
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠DFA=∠AOB,
∴∠DAF=∠ABO,
∴△DFA∽△AOB
![]()
![]()
![]()
∵E为AB的中点,∠AOB=90°,
∴AE=OE,
∴∠AOE=∠OAE,
∴△DFO∽△BOA,
![]()
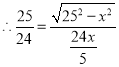
解得![]() 舍去,
舍去,
![]()
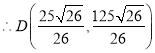 ,故③正确.
,故③正确.
故答案为:②③.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3