题目内容
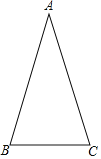
【题目】 如图，在△ABC中，AB＝AC．
（1）用尺规作图法在AC边上找一点D，使得BD＝BC（保留作图痕迹，不要求写作法）：
（2）若∠A＝30°，求∠ABD的大小．
【答案】45°．
【解析】
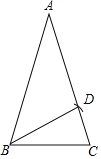
（1）以B点为圆心，BC为半径画弧交AC于D；
（2）先根据等腰三角形的性质和三角形内角和定理计算出∠ABC＝∠C＝75°，再利用等腰三角形的性质得到∠BDC＝∠C＝75°，然后根据三角形外角性质求∠ABD的度数．
解：（1）如图，点D为所作；
（2）∵AB＝AC，
∴∠ABC＝∠C＝
（180°﹣∠A）＝（180°﹣30°）＝75°，
∵BD＝BC，
∴∠BDC＝∠C＝75°，
∵∠BDC＝∠A+∠ABD，
∴∠ABD＝75°﹣30°＝45°．
练习册系列答案
相关题目
【题目】某校团委组织“阳光助残”献爱心捐款活动，九年级（2）班学生捐款如表：
捐款金额（元） | 5 | 10 | 15 | 20 |
人数（人） | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是（ ）
A. 10元，15元 B. 15元，15元 C. 10元，20元 D. 16元，17元
