题目内容
【题目】如图,在平面在角坐标系中,抛物线y=x2-2x-3与x轴交与点A,B(点A在点B的左侧)交y轴于点C,点D为抛物线的顶点,对称轴与x轴交于点E.
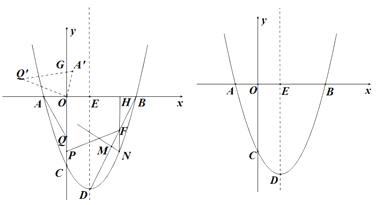
(1)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当MN取得最大值时,求HF+FP+![]() PC的最小值;
PC的最小值;
(2)在(1)中,当MN取得最大值HF+FP+1/3PC取得小值时,把点P向上平移个![]() 单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度
单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度![]() (0°<
(0°<![]() <360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得
<360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得![]() ?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,Q的坐标(
;(2)存在,Q的坐标(![]() ,﹣
,﹣![]() ),(
),(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() )
)
【解析】
(1)先确定点F的位置,可设点N(m,m2-2m-3),则点F(m,2m-6),可得|NF|=(2m-6)-(m2-2m-3)=-m2+4m-3,根据二次函数的性质得m=![]() 时,NF取到最大值,此时HF=2, F(2,-2),在x轴上找一点K(
时,NF取到最大值,此时HF=2, F(2,-2),在x轴上找一点K(![]() ,0),连接CK,过点F作CK的垂线交CK于点J,交y轴于点P,
,0),连接CK,过点F作CK的垂线交CK于点J,交y轴于点P,![]() ,直线KC的解析式为:
,直线KC的解析式为:![]() ,从而得到直线FJ 的解析式为:
,从而得到直线FJ 的解析式为:![]() 联立解出点J(
联立解出点J(![]() ,
, ![]()
)得FP+![]() PC的最小值即为FJ的长,且
PC的最小值即为FJ的长,且![]() , 最后得出
, 最后得出![]() ;(2)由题意可得出点Q(0,-2),A2=
;(2)由题意可得出点Q(0,-2),A2=![]() ,应用“直角三角形斜边上的中线等于斜边上的一半”取AQ的中点G,连接OG,则OG=GQ=
,应用“直角三角形斜边上的中线等于斜边上的一半”取AQ的中点G,连接OG,则OG=GQ=![]() AQ=
AQ=![]() ,此时,∠AQ0=∠GOQ,把△AOQ绕点O顺时针旋转一定的角度
,此时,∠AQ0=∠GOQ,把△AOQ绕点O顺时针旋转一定的角度![]() (0°<
(0°<![]() <360°),得到△A'OQ',其中边A’Q’交坐标轴于点G,则用0G=GQ’,分四种情况求解即可.
<360°),得到△A'OQ',其中边A’Q’交坐标轴于点G,则用0G=GQ’,分四种情况求解即可.
解:(1)如图1

∵抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B的左侧),交y轴于点C
∴令y=0解得:x1=﹣1,x2=3,令x=0,解得:y=﹣3,
∴A(﹣1,0),B(3,0),C(0,﹣3)
∵点D为抛物线的顶点,且![]() ﹣4
﹣4
∴点D的坐标为D(1,﹣4)
∴直线BD的解析式为:y=2x﹣6,
由题意,可设点N(m,m2﹣2m﹣3),则点F(m,2m﹣6)
∴|NF|=(2m﹣6)﹣(m2﹣2m﹣3)=﹣m2+4m﹣3
∴当m=![]() =2时,NF 取到最大值,此时MN取到最大值,此时HF=2,
=2时,NF 取到最大值,此时MN取到最大值,此时HF=2,
此时,N(2,﹣3),F(2,﹣2),H(2,0)
在x轴上找一点K(![]() ,0),连接CK,过点F作CK的垂线交CK于点J点,交y轴于点P,
,0),连接CK,过点F作CK的垂线交CK于点J点,交y轴于点P,
∴sin∠OCK=![]() ,直线KC的解析式为:
,直线KC的解析式为:![]() ,且点F(2,﹣2),
,且点F(2,﹣2),
∴PJ=![]() PC,直线FJ的解析式为:
PC,直线FJ的解析式为:![]()
∴点J(![]() ,
, ![]() )
)
∴FP+![]() PC的最小值即为FJ的长,且
PC的最小值即为FJ的长,且![]()
∴![]() ;
;
(2)由(1)知,点P(0, ![]() ),
),
∵把点P向上平移![]() 个单位得到点Q
个单位得到点Q
∴点Q(0,﹣2)
∴在Rt△AOQ中,∠AOG=90°,AQ=![]() ,取AQ的中点G,连接OG,则OG=GQ=
,取AQ的中点G,连接OG,则OG=GQ=![]() AQ=
AQ=![]() ,此时,∠AQO=∠GOQ
,此时,∠AQO=∠GOQ
把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G
①如图2

G点落在y轴的负半轴,则G(0,﹣![]() ),过点Q'作Q'I⊥x轴交x轴于点I,且∠GOQ'=∠Q'
),过点Q'作Q'I⊥x轴交x轴于点I,且∠GOQ'=∠Q'
则∠IOQ'=∠OA'Q'=∠OAQ,
∵sin∠OAQ=![]() =
=![]() =
=![]()
∴![]() ,解得:|IO|=
,解得:|IO|=![]()
∴在Rt△OIQ'中根据勾股定理可得|OI|=![]()
∴点Q'的坐标为Q'(![]() ,﹣
,﹣![]() );
);
②如图3,![]()

当G点落在x轴的正半轴上时,同理可得Q'(![]() ,
,![]() )
)
③如图4

当G点落在y轴的正半轴上时,同理可得Q'(﹣![]() ,
,![]() )
)
④如图5
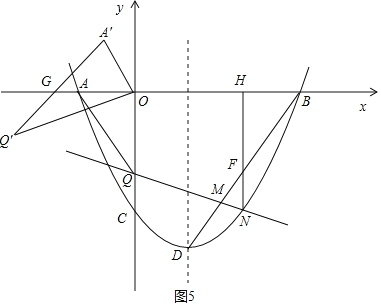
当G点落在x轴的负半轴上时,同理可得Q'(﹣![]() ,﹣
,﹣![]() )
)
综上所述,所有满足条件的点Q′的坐标为:(![]() ,﹣
,﹣![]() ),(
),(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() )
)