题目内容
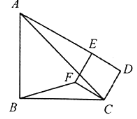
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .
.
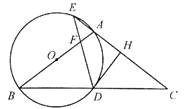
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若⊙![]() 的半径为4,①当
的半径为4,①当![]() 时,求
时,求![]() 的长(结果保留π);②当
的长(结果保留π);②当![]() 时,求线段
时,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)①![]() 的长=
的长=![]() ;②AF=
;②AF=![]() .
.
【解析】
(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;
(2)①根据等腰三角形的性质的∠EAF=∠EAF,设∠B=∠C=α,得到∠EAF=∠EFA=2α,根据三角形的内角和得到∠B=36°,求得∠AOD=72°,根据弧长公式即可得到结论;
②连接AD,根据圆周角定理得到∠ADB=∠ADC=90°,解直角三角形得到AD=![]() ,根据相似三角形的性质得到AH=3,于是得到结论.
,根据相似三角形的性质得到AH=3,于是得到结论.
(1)连接OD,如图,
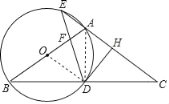
∵OB=OD,
∴△ODB是等腰三角形,
∠OBD=∠ODB①,
在△ABC中,∵AB=AC,
∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是圆O的切线;
(2)①∵AE=EF,
∴∠EAF=∠EAF,
设∠B=∠C=α,
∴∠EAF=∠EFA=2α,
∵∠E=∠B=α,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°,
∴∠AOD=72°,
∴![]() 的长=
的长=![]() ;
;
②连接AD,
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
∵⊙O的半径为4,
∴AB=AC=8,
∵![]() ,
,
∴![]() ,
,
∴AD=2![]() ,
,
∵AD⊥BC,DH⊥AC,
∴△ADH∽△ACD,
∴![]() ,
,
∴![]() ,
,
∴AH=3,
∴CH=5,
∵∠B=∠C,∠E=∠B,
∴∠E=∠C,
∴DE=DC,∵DH⊥AC,
∴EH=CH=5,
∴AE=2,
∵OD∥AC,
∴∠EAF=∠FOD,∠E=∠FDO,
∴△AEF∽△ODF,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() .
.

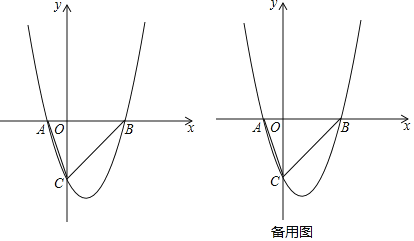
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3