题目内容
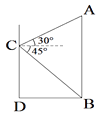
【题目】某数学兴趣小组的同学在一次活动中,为了测量某建筑物AB的高,他们来到另一建筑物CD上的点C处进行观察,如图所示,他们测得建筑物AB顶部A的仰角为30°,底部B的俯角为45°,已知建筑物AB、CD的距离DB为12m,求建筑物AB的高.
【答案】AB=(4![]() +12)m.
+12)m.
【解析】
过点C作AB的垂线,垂足为E,根据题意可得出四边形CDBE是矩形,再由CD=12m,∠ECB=45°可知BE=CE=12m,由AE=CEtan30°得出AE的长,进而可得出结论.
过点C作AB的垂线,垂足为E,
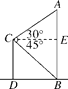
又∵CD⊥BD,AB⊥BD,∠ECB=45°,
∴四边形CDBE是正方形.
∵BD=12m,∴BD=CE=BE=12m,
∴AE=CE·tan30°=12×![]() =4
=4![]() (m),
(m),
∴AB=(4![]() +12)m.
+12)m.

练习册系列答案
相关题目