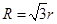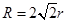题目内容
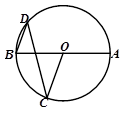
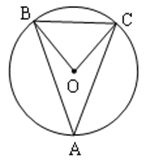
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
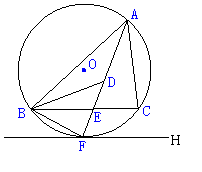
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.

(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
(1)证明见解析;(2)证明见解析;(3)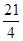 .
.
 .
.试题分析:(1)连接OF,通过切线的性质证OF⊥FH,进而由FH∥BC,得OF⊥BC,即可由垂径定理得到F是弧BC的中点,根据圆周角定理可得∠BAF=∠CAF,由此得证;
(2)求BF=FD,可证两边的对角相等;易知∠DBF=∠DBC+∠FBC,∠BDF=∠BAD+∠ABD;观察上述两个式子,∠ABD、∠CBD是被角平分线平分∠ABC所得的两个等角,而∠CBF和∠DAB所对的是等弧,由此可证得∠DBF=∠BDF,即可得证;
(3)由EF、DE的长可得出DF的长,进而可由(2)的结论得到BF的长;然后证△FBE∽△FAB,根据相似三角形得到的成比例线段,可求出AF的长,即可由AD=AF-DF求出AD的长.
试题解析:(1)证明:连接OF
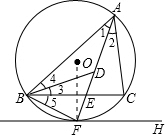
∵FH是⊙O的切线
∴OF⊥FH
∵FH∥BC,
∴OF垂直平分BC
∴
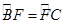 ,
,∴∠1=∠2,
∴AF平分∠BAC
(2)证明:由(1)及题设条件可知
∠1=∠2,∠4=∠3,∠5=∠2
∴∠1+∠4=∠2+∠3
∴∠1+∠4=∠5+∠3
∵∠1+∠4=∠BDF,∠5+∠3=∠FBD,
∴∠BDF=∠FBD,
∴BF=FD(6分)
(3)解:在△BFE和△AFB中
∵∠5=∠2=∠1,∠AFB=∠AFB,
∴△BFE∽△AFB
∴
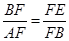 ,
,∴BF2=FE•FA
∴
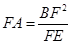 ,EF=4,BF=FD=EF+DE=4+3=7,
,EF=4,BF=FD=EF+DE=4+3=7,∴
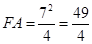
∴AD=AF-DF=AF-(DE+EF)=
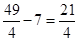 .
.考点: 1.切线的性质;2.角平分线的性质;3.垂径定理;4.相似三角形的判定与性质.

练习册系列答案
相关题目
 )上,再按顺时针方向绕点B翻转到△
)上,再按顺时针方向绕点B翻转到△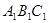 的位置(
的位置(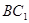 在
在 的位置,其平移的距离为线段AC的长度(此时
的位置,其平移的距离为线段AC的长度(此时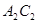 恰好靠在墙边)。
恰好靠在墙边)。
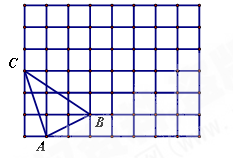
 ,画出旋转后的△A1B2C2;
,画出旋转后的△A1B2C2;