Question

【题目】如图：长方形ABCD中，AD=10，AB=4，点Q是BC的中点，点P在AD边上运动，当△BPQ是等腰三角形时，AP的长为 .

Answer 1

【答案】2或2.5或3或8．

【解析】

试题∵AD=10，点Q是BC的中点，∴BQ=BC=×10=5，

如图1，PQ=BQ=5时，过点P作PE⊥BC于E，

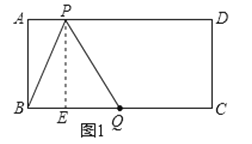
根据勾股定理，QE=，

∴BE=BQ﹣QE=5﹣3=2，∴AP=BE=2；

②如图2，BP=BQ=5时，过点P作PE⊥BC于E，

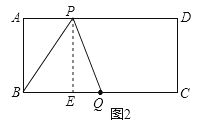
根据勾股定理，BE=，∴AP=BE=3；

③如图3，PQ=BQ=5且△PBQ为钝角三角形时，

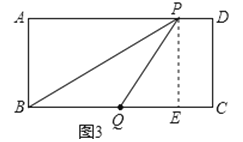
BE=QE+BQ=3+5=8，AP=BE=8，

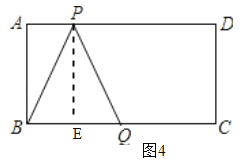
④若BP=PQ，如图4，过P作PE⊥BQ于E，则BE=QE=2.5，∴AP=BE=2.5．

综上所述，AP的长为2或3或8或2.5．

故答案为：2或3或8或2.5．