题目内容
【题目】在正方形ABCD中,点P是直线BC上的一点,连接AP,将线段PA绕点P顺时针旋转90°,得到线段PE,连接CE.
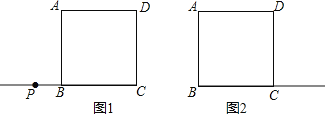
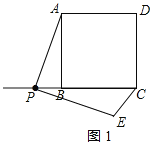
(1)如图1,点P在线段CB的延长线上.
①请根据题意补全图形;
②用等式表示BP和CE的数量关系,并证明.
(2)若点P在射线BC上,直接写出CE,CP,CD三条线段的数量关系为 .
【答案】(1)①详见解析;②CE=![]() BP,证明详见解析;(2)CE=
BP,证明详见解析;(2)CE=![]() (CD﹣CP)或CE=
(CD﹣CP)或CE=![]() (CD+CP) .
(CD+CP) .
【解析】
(1)①据题意补全图形即可;
②作EM⊥BC于M,证明△ABP≌△PME(AAS),得出AB=PM,BP=ME,证明△CEM是等腰直角三角形,得出CE=![]() ME,即可得出结论;
ME,即可得出结论;
(2)①当点P在线段BC上时,在BA上截取BM=BP.则△PBM是等腰直角三角形,证明△PCE≌△AMP(SAS),得出CE=PM,即可得出结论;
②当点P在线段BC的延长线上时,在BA上截取BM=BP.则△PBM是等腰直角三角形,PM=![]() BP.证明△PCE≌△AMP(SAS),得出CE=PM,即可得出结论.
BP.证明△PCE≌△AMP(SAS),得出CE=PM,即可得出结论.
解:(1)①据题意补全图形,如图1所示:
②CE=![]() BP,理由如下:
BP,理由如下:
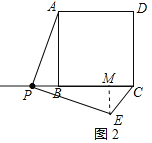
作EM⊥BC于M,如图2所示:
由旋转的性质得:PE=PA,∠APE=90°,
即∠APB+∠EPM=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABP=90°,
∴∠APB+∠PAB=90°,
∴∠PAB=∠EPM,
在△ABP和△PME中,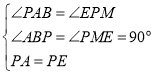 ,
,
∴△ABP≌△PME(AAS),
∴AB=PM,BP=ME,
∴PM=BC,
∴BP=CM=ME,
∴△CEM是等腰直角三角形,
∴CE=![]() ME,
ME,
∴CE=![]() BP;
BP;
(2)分两种情况:
①当点P在线段BC上时,CE=![]() (CD﹣CP),理由如下:
(CD﹣CP),理由如下:
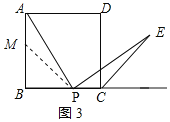
在BA上截取BM=BP,连接PM,如图3所示:
则△PBM是等腰直角三角形,
∴PM=![]() BP,∠BMP=∠BPM=45°,
BP,∠BMP=∠BPM=45°,
∵AB=BC,
∴AM=PC,
由旋转的性质得:PE=PA,∠APE=90°,
∴∠APM+∠CPE=180°﹣90°﹣45°=45°,
又∵∠MAP+∠APM=∠BMP=45°,
∴∠MAP=∠CPE,
在△PCE和△AMP中,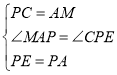 ,
,
∴△PCE≌△AMP(SAS),
∴CE=PM,
∵CD﹣PC=BC﹣PC=BP,
∴CE=PM=![]() BP=
BP=![]() (CD﹣CP);
(CD﹣CP);
②当点P在线段BC的延长线上时,CE=![]() (CD+CP),理由如下:
(CD+CP),理由如下:
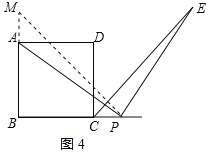
在BA上截取BM=BP,连接PM,如图4所示:
则△PBM是等腰直角三角形,PM=![]() BP.
BP.
∵四边形ABCD是正方形,
∴AB=BC,∠DAM=∠BAD=90°,AD∥BC,
∴AM=PC,∠DAP=∠APB,
由旋转的性质得:PE=PA,∠APE=90°,
∴∠PAM=∠EPC,
在△PCE和△AMP中,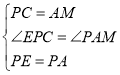 ,
,
∴△PCE≌△AMP(SAS),
∴CE=PM,
∵CD+CP=BC+CP=BP,
∴CE=PM=![]() BP=
BP=![]() (CD+CP);
(CD+CP);
故答案为:CE=![]() (CD﹣CP)或CE=
(CD﹣CP)或CE=![]() (CD+CP).
(CD+CP).

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案