题目内容
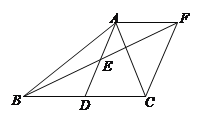
【题目】如图 1，在正方形 ABCD 中，对角线 AC, BD 交于点 O ，点 E 在 AB 上，点 F 在 BC 的延长线上，且 AE CF .连接 EF 交 AC 于点 P, 分别连接 DE, DF .
（1）求证： ADE CDF ;
（2）求证： PE PF ;
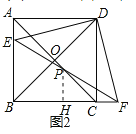
（3）如图 2，若 PE BE, 则
的值是 .（直接写出结果即可）.
【答案】（1）证明见解析；（2）证明见解析；（3）
.
【解析】
（1）根据
证明即可；
（2）作
交
的延长线于
，根据四边形
是正方形，即可得到
，再根据
得到
，从而
，则
，根据
可证
，即可得证
；
（3）如图2中，作
于，首先证明
，设
，则
，
，求出
即可解决问题.
（1）证明：
四边形是正方形，
，
，
，
；
（2）证明：作交的延长线于，
四边形是正方形，
，
，
，
，
，
，
，
，
；
（3）如图2中，作于，
由（2）可知：，
，
，
，
，
，
，
，
，
，
，
设，则，，
，
.
故答案为：.
练习册系列答案
相关题目
【题目】某校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中只选一类最喜爱的电视节目，以下是根据调查结果绘制的不完整统计表，根据表中信息，回答下列问题：
喜爱的电视节目类型 | 人数 | 频率 |
新闻 | 4 | 0.08 |
体育 | / | / |
动画 | 15 | / |
娱乐 | 18 | 0.36 |
戏曲 | / | 0.06 |
(1)本次共调查了_______名学生，若将各类电视节目喜爱的人数所占比例绘制成扇形统计图，则“喜爱动画”对应扇形的圆心角度数是_______；
(2)该校共有2000名学生，根据调查结果估计该校“喜爱体育”节目的学生人数；
(3)在此次问卷调查中，甲、乙两班分别有
人喜爱新闻节目，若从这
人中随机抽取人去参加“新闻小记者”培训，求抽取的人来自不同班级的概率．
