ЬтФПФкШн
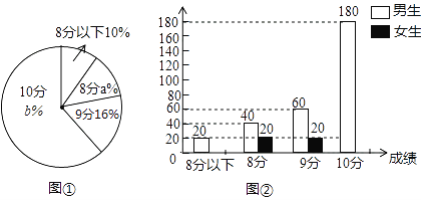
ЁОЬтФПЁПФГаЃзщжЏ360УћЪІЩњЭтГіЛюЖЏЃЌМЦЛЎзтгУМзЁЂввСНжжаЭКХЕФПЭГЕЃЛОСЫНтЃЌМзГЕУПСОзюЖрФмди40ШЫКЭ16МўааРюЃЌввГЕУПСОзюЖрФмди30ШЫКЭ20МўааРюЃЎ
ЃЈ1ЃЉвбжЊЪІЩњааРюДђАќКѓЙВга164МўЃЌШєзтгУ10СОМзЁЂввСНжжаЭКХЕФПЭГЕЃЌЧыФуАяжњЩшМЦГіИУаЃЫљгаПЩааЕФзтГЕЗНАИЃЛ
ЃЈ2ЃЉШєЪІЩњааРюДђАќКѓЙВгаmМўЃЌЧв170 < m Ём 184ЃЌШчЙћЫљзтГЕСОИеКУАбЫљгаЪІЩњКЭааРюдизпЃЈУПСОГЕОљвдзюЖрГадиСПдиТњЃЉЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁП(1)МћНтЮі;(2)176.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЩшзтгУМзГЕxСОЃЌдђввГЕ![]() СОЃЌИљОнИљОнГЕСОЫљдиШЫЪ§ВЛЩйгк360ШЫЃЌааРюМўЪ§ВЛЩйгк164ПЩСаГіЗНГЬзщ
СОЃЌИљОнИљОнГЕСОЫљдиШЫЪ§ВЛЩйгк360ШЫЃЌааРюМўЪ§ВЛЩйгк164ПЩСаГіЗНГЬзщ![]() ,ОнДЫЧѓЕУxЕФШЁжЕЗЖЮЇЃЌНсКЯxЪЧећЪ§НтД№МДПЩЃЛ
,ОнДЫЧѓЕУxЕФШЁжЕЗЖЮЇЃЌНсКЯxЪЧећЪ§НтД№МДПЩЃЛ
ЃЈ2ЃЉЩшзтгУМзГЕyСОЃЌввГЕzСОЃЌИљОнЬтвтЕУЃК40y + 30z = 360ЃЌm = 16y + 20z
ЛЏМђЕУЃК4y = 36Љ3zЃЌДњШыm = 16y + 20zЕУЃКm = 144 + 8z
НсКЯmЕФШЁжЕЗЖЮЇПЩЕУГі3.25 < z Ём 5ЃЌИљОнzЁЂyЪЧЗЧИКећЪ§вдМА4y = 36Љ3zЃЌЧѓЕУzЁЂyМДПЩ.
ЯъНтЃКЃЈ1ЃЉЩшзтгУМзГЕxСОЃЌдђввГЕ![]() СОЃЎИљОнЬтвтЕУЃК
СОЃЎИљОнЬтвтЕУЃК
![]() ЃЌНтЕУЃК6 Ём x Ём 9ЃЎ
ЃЌНтЕУЃК6 Ём x Ём 9ЃЎ
ЁпxЪЧећЪ§
Ёрx = 6Лђ7Лђ8Лђ9ЃЎ
ЙВгаЫФжжЗНАИЃК
ЂйЕБМзГЕзт6СОЃЌдђввГЕзт4СОЃЛЂкЕБМзГЕзт7СОЃЌдђввГЕзт3СОЃЛ
ЂлЕБМзГЕзт8СОЃЌдђввГЕзт2СОЃЛЂмЕБМзГЕзт9СОЃЌдђввГЕзт1СОЃЛ
ЃЈ2ЃЉЩшзтгУМзГЕyСОЃЌввГЕzСОЃЌИљОнЬтвтЕУЃК40y + 30z = 360ЃЌm = 16y + 20z
ЛЏМђЕУЃК4y = 36Љ3zЃЌДњШыm = 16y + 20zЕУЃКm = 144 + 8z
Ёп170 < m Ём 184
Ёр170 < 144+8z Ём 184
Ёр3.25 < z Ём 5
ЁпzЁЂyЪЧЗЧИКећЪ§
Ёрz = 4ЃЌy = 6ЃЌ
Ёрm = 176ЃЎ

ЁОЬтФПЁПЮЊСЫгНгеуНЪЁжааЁбЇЩњНЁПЕЬхжЪВтЪдЃЌФГбЇаЃПЊеЙЁАНЁПЕаЃдАЃЌбєЙтЬјЩўЁБЛюЖЏЃЌЮЊДЫбЇаЃзМБИЙКжУAЃЌBЃЌCШ§жжЬјЩў.вбжЊФГГЇМвЕФЬјЩўЕФЙцИёгыМлИёШчЯТБэЃК
AЩўзг | BЩўзг | CЩўзг | |
ГЄЖШ(Уз) | 8 | 6 | 4 |
ЕЅМл(дЊ/Ьѕ) | 12 | 8 | 6 |
(1)вбжЊЙКТђAЃЌBСНжжЩўзгЙВ20ЬѕЛЈСЫ180дЊЃЌЮЪAЃЌBСНжжЩўзгИїЙКТђСЫЖрЩйЬѕЃП
(2)ШєИУГЇМвгавЛИљГЄ200УзЕФЩўзгЃЌЯжНЋЦфВУГЩAЃЌCСНжжЩўзгЯњЪлзмМлЮЊ240дЊЃЌдђЪЃгрЕФЩўзгГЄЖШзюЖрПЩМгЙЄМИЬѕBжжЩўзгЃП
(3)ШєИУГЇМвгавЛИљГЄ200УзЕФЩўзгЃЌЯжНЋЦфВУГЩAЃЌBЃЌCШ§жжЩўзгЙВ40Ьѕ(УЛгаЪЃгр)ЯњЪлИјбЇаЃЃЌбЇаЃвЊЧѓAжжЩўзгЕФЪ§СПЩйгкBжжЩўзгЕФЪ§СПЕЋВЛЩйгкBжжЩўзгЕФЪ§СПЕФвЛАыЃЌЧыжБНгаДГіЫљгаЕФВУМєЗНАИ.