题目内容
【题目】(建立概念)如下图,A、B为数轴上不重合的两定点,点P也在该数轴上,我们比较线段![]() 和
和![]() 的长度,将较短线段的长度定义为点P到线段
的长度,将较短线段的长度定义为点P到线段![]() 的“靠近距离”.特别地,若线段
的“靠近距离”.特别地,若线段![]() 和
和![]() 的长度相等,则将线段
的长度相等,则将线段![]() 或
或![]() 的长度定义为点P到线段
的长度定义为点P到线段![]() 的“靠近距离”.
的“靠近距离”.
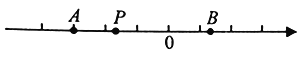
(概念理解)如下图,数轴的原点为O,点A表示的数为![]() ,点B表示的数为4.
,点B表示的数为4.
(1)点O到线段![]() 的“靠近距离”为________;
的“靠近距离”为________;
(2)点P表示的数为m,若点P到线段![]() 的“靠近距离”为3,则m的值为_________;
的“靠近距离”为3,则m的值为_________;

(拓展应用)(3)如下图,在数轴上,点P表示的数为![]() ,点A表示的数为
,点A表示的数为![]() ,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为
,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为![]() 秒,当点P到线段
秒,当点P到线段![]() 的“靠近距离”为3时,求t的值.
的“靠近距离”为3时,求t的值.

【答案】(1)2;(2)5或1或7;(3)![]() 或
或![]()
【解析】
(1)根据题意OA的长度即为所求;(2)分三种情况进行讨论,①当点P位于A点左侧;②点P位于线段AB上;③点P位于B点右侧,分别求解;(3)分情况讨论,当PA=3或PB=3时,分别求解.
解:(1)由题意OA=2;OB=4
∴点O到线段![]() 的“靠近距离”为2
的“靠近距离”为2
故答案为:2;
(2)①当点P位于A点左侧时,点P表示-2-3=-5;
②点P位于线段AB上时,点P表示-2+3=1,此时PA=PB=1
③点P位于B点右侧时,点P表示4+3=7
∴m=5或1或7
故答案为:5或1或7;
(3)当PA=3时, 可得![]() ,或
,或![]() ,
,
解得![]() .
.
而当![]() 时,PB=14-4×3=2,
时,PB=14-4×3=2,![]() <
<![]() ,点P到线段AB的“靠近距离”为2,不符合题意.
,点P到线段AB的“靠近距离”为2,不符合题意.
所以![]() .
.
当PB=3时, 可得![]() ,或
,或![]() ,
,
解得![]() .
.
而当![]() 时,PA=
时,PA=![]() ,PA<PB,点P到线段AB的“靠近距离”为
,PA<PB,点P到线段AB的“靠近距离”为![]() ,不符合题意.
,不符合题意.
所以![]() .
.
综上所述,所以![]() 或
或![]() .
.

练习册系列答案
相关题目