ЬтФПФкШн
ЁОЬтФПЁПЁАЗжПщМЦЪ§ЗЈЁБЃКЖдгаЙцТЩЕФЭМаЮНјааМЦЪ§ЪБЃЌгааЉЬтПЩвдВЩгУЁАЗжПщМЦЪ§ЁБЕФЗНЗЈЃЎ
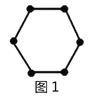
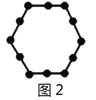
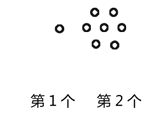
Р§ШчЃКЭМ1га6ИіЕуЃЌЭМ2га12ИіЕуЃЌЭМ3га18ИіЕуЃЌЁЃЌАДДЫЙцТЩЃЌЧѓЭМ8ЁЂЭМ![]() гаЖрЩйИіЕуЃП
гаЖрЩйИіЕуЃП
ЮвУЧНЋУПИіЭМаЮЗжГЩЭъШЋЯрЭЌЕФ6ПщЃЌУППщКкЕуЕФИіЪ§ЯрЭЌЃЈШчЭМЃЉЃЌетбљЭМ1жаКкЕуИіЪ§ЪЧ![]() ИіЃЛЭМ2жаКкЕуИіЪ§ЪЧ
ИіЃЛЭМ2жаКкЕуИіЪ§ЪЧ![]() ИіЃЛЭМ3жаКкЕуИіЪ§ЪЧ
ИіЃЛЭМ3жаКкЕуИіЪ§ЪЧ![]() ИіЃЛЁЃЌЫљвдШнвзЧѓГіЭМ8ЁЂЭМ
ИіЃЛЁЃЌЫљвдШнвзЧѓГіЭМ8ЁЂЭМ![]() жаКкЕуЕФИіЪ§ЗжБ№ЪЧ______ЁЂ_________ЃЎ
жаКкЕуЕФИіЪ§ЗжБ№ЪЧ______ЁЂ_________ЃЎ

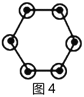
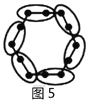
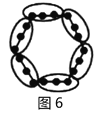
ЧыФуВЮПМвдЩЯЁАЗжПщМЦЪ§ЗЈЁБЃЌЯШНЋЯТУцЕФЕуеѓНјааЗжПщЃЈЛдкД№ЬтПЈЩЯЃЉЃЌдйЭъГЩвдЯТЮЪЬтЃК
ЃЈ1ЃЉЕк6ИіЕуеѓжага______ИідВШІЃЛЕк![]() ИіЕуеѓжага______ИідВШІЃЎ
ИіЕуеѓжага______ИідВШІЃЎ
ЃЈ2ЃЉаЁдВШІЕФИіЪ§ЛсЕШгк331Т№ЃПЧыЧѓГіЪЧЕкМИИіЕуеѓЃЎ


ЁОД№АИЁП48ЃЛ6nЃЛЃЈ1ЃЉ91ЃЛ![]() ЃЛЃЈ2ЃЉЛсЃЛЕк11ИіЕуеѓ
ЃЛЃЈ2ЃЉЛсЃЛЕк11ИіЕуеѓ
ЁОНтЮіЁП
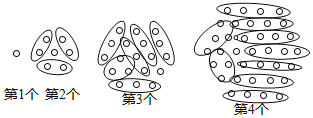
ИљОнЙцТЩПЩЧѓЕУЭМ8жаКкЕуИіЪ§КЭЭМnжаКкЕуИіЪ§ЃЛ
ЃЈ1ЃЉЕк2ИіЭМжа2ЮЊвЛПщЃЌЗжЮЊ3ПщЃЌгр1ЃЌЕк3ИіЭМжа3ЮЊвЛПщЃЌЗжЮЊ6ПщЃЌгр1ЃЛАДДЫЙцТЩЕУЃКЕк6ИіЕуеѓжа6ЮЊвЛПщЃЌЗжЮЊ15ПщЃЌгр1ЃЌЕУЕкnИіЕуеѓжагаЃКnЁС3ЃЈn-1ЃЉ+1=3n2-3n+1ЃЛ
ЃЈ2ЃЉСю3n2-3n+1=331ЃЌЗНГЬгаНтдђДцдкетбљЕФЕуеѓЃЌОнДЫНтД№.
НтЃКЭМ8жаКкЕуИіЪ§ЪЧ6ЁС8=48ИіЃЛЭМnжаКкЕуИіЪ§ЪЧ6nИіЃЛ
ЃЈ1ЃЉШчЭМЫљЪОЃКЕк1ИіЕуеѓжагаЃК1ИіЃЌ
Ек2ИіЕуеѓжагаЃК2ЁС3+1=7ИіЃЌ
Ек3ИіЕуеѓжагаЃК3ЁС6+1=19ИіЃЌ
Ек4ИіЕуеѓжагаЃК4ЁС9+1=37ИіЃЌ
Ек5ИіЕуеѓжагаЃК5ЁС12+1=61ИіЃЌ
Ек6ИіЕуеѓжагаЃК6ЁС15+1=91ИіЃЌ
Ё
ЕкnИіЕуеѓжагаЃКnЁС3ЃЈn-1ЃЉ+1=3n2-3n+1ЃЌ
ЙЪД№АИЮЊЃК91ЃЌ3n2-3n+1ЃЛ
ЃЈ2ЃЉ3n2-3n+1=331ЃЌ
n2-n-110=0ЃЌ
ЃЈn-11ЃЉЃЈn+10ЃЉ=0ЃЌ
n1=11ЃЌn2=-10ЃЈЩсЃЉЃЌ
ЁраЁдВШІЕФИіЪ§ЛсЕШгк331ЃЌЫќЪЧЕк11ИіЕуеѓЃЎ

ЁОЬтФПЁППьЕнЙЋЫОЮЊЬсИпПьЕнЗжМ№ЕФЫйЖШЃЌОіЖЈЙКТђЛњЦїШЫРДДњЬцШЫЙЄЗжМ№ЃЌСНжжаЭКХЕФЛњЦїШЫЕФЙЄзїаЇТЪКЭМлИёШчБэЃК
аЭКХ | Мз | вв |
УПЬЈУПаЁЪБЗжМ№ПьЕнМўЪ§(Мў) | 1000 | 800 |
УПЬЈМлИё(ЭђдЊ) | 5 | 3 |
ИУЙЋЫОМЦЛЎЙКТђетСНжжаЭКХЕФЛњЦїШЫЙВ10ЬЈЃЌВЂЧвЪЙет10ЬЈЛњЦїШЫУПаЁЪБЗжМ№ПьЕнМўЪ§змКЭВЛЩйгк8500Мў
(1)ЩшЙКТђМзжжаЭКХЕФЛњЦїШЫxЬЈЃЌЙКТђет10ЬЈЛњЦїШЫЫљЛЈЕФЗбгУЮЊyЭђдЊЃЌЧѓyгыxжЎМфЕФЙиЯЕЪНЃЛ
(2)ЙКТђМИЬЈМзжжаЭКХЕФЛњЦїШЫЃЌФмЪЙЙКТђет10ЬЈЛњЦїШЫЫљЛЈзмЗбгУзюЩйЃПзюЩйЗбгУЪЧЖрЩйЃП
ЁОЬтФПЁПФГЦЗХЦЕчФдЯњЪлЙЋЫОгагЊЯњдБ14ШЫЃЌЯњЪлВПЮЊжЦЖЈгЊЯњШЫдБдТЯњЪлЕчФдЖЈЖюЃЌЭГМЦСЫет14ШЫФГдТЕФЯњЪлСПШчЯТЃЈЕЅЮЛЃКЬЈЃЉЃК
ЯњЪлСП | 200 | 170 | 130 | 80 | 50 | 40 |
ШЫЪ§ | 1 | 1 | 2 | 5 | 3 | 2 |
ЃЈ1ЃЉИУЙЋЫОгЊЯњдБЯњЪлИУЦЗХЦЕчФдЕФдТЯњЪлЦНОљЪ§ЪЧ ЬЈЃЌжаЮЛЪ§ЪЧ ЬЈЃЌжкЪ§ЪЧ ЬЈЃЎ
ЃЈ2ЃЉЯњЪлВПОРэАбУПЮЛгЊЯњдБдТЯњЪлСПЖЈЮЊ90ЬЈЃЌФуШЯЮЊЪЧЗёКЯРэЃПЫЕУїРэгЩЃЎ
ЁОЬтФПЁПЃЈЮЪЬтЃЉШєa+bЃН10ЃЌдђabЕФзюДѓжЕЪЧЖрЩйЃП
ЃЈЬНОПЃЉ
ЬНОПвЛЃКЕБaЉbЃН0ЪБЃЌЧѓabжЕЃЎ
ЯдШЛДЫЪБЃЌaЃНbЃН5ЃЌдђabЃН5ЁС5ЃН25
ЬНОПЖўЃКЕБaЉbЃНЁР1ЪБЃЌЧѓabжЕЃЎ
ЂйaЉbЃН1ЃЌдђaЃНb+1ЃЌ
гЩвбжЊЕУb+1+bЃН10
НтЕУ bЃН![]() ЃЌ
ЃЌ
aЃНb+lЃН![]() +1ЃН
+1ЃН![]()
дђabЃН![]() ЃН
ЃН![]()
ЂкaЉbЃНЉ1ЃЌМДbЉaЃН1ЃЌгЩЂйПЩЕУЃЌbЃН![]() ЃЌaЃН
ЃЌaЃН![]()
дђabЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЬНОПШ§ЃКЕБaЉbЃНЁР2ЪБЃЌЧѓabжЕЃЈЗТееЩЯЪіЗНЗЈЃЌаДГіЬНОПЙ§ГЬЃЉЃЎ
ЬНОПЫФЃКЭъГЩЯТБэЃК
aЉb | Ё | Љ3 | Љ2 | Љ1 | 0 | 1 | 2 | 3 | Ё |
ab | Ё | ЁЁ ЁЁ | ЁЁ ЁЁ |
| 25 |
| ЁЁ ЁЁ | ЁЁ ЁЁ | Ё |
ЃЈНсТлЃЉШєa+bЃН10ЃЌдђabЕФзюДѓжЕЪЧЁЁ ЁЁЃЈЙлВьЩЯУцБэИёЃЌжБНгаДГіНсЙћЃЉЃЎ
ЃЈЭиеЙЃЉШєa+bЃНmЃЌдђabЕФзюДѓжЕЪЧЁЁ ЁЁЃЎ
ЃЈгІгУЃЉгУвЛИљГЄЮЊ12mЕФЬњЫПЮЇГЩвЛИіГЄЗНаЮЃЌетИіГЄЗНаЮУцЛ§ЕФзюДѓжЕЪЧЁЁ ЁЁm2ЃЎ