题目内容
【题目】设函数y=k1x+![]() ,且k1k2≠0,自变量x与函数值y满足以下表格:
,且k1k2≠0,自变量x与函数值y满足以下表格:
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
(1)根据表格直接写出y与x的函数表达式及自变量x的取值范围______
(2)补全上面表格:m=______,n=______;在如图所示的平面直角坐标系中,请根据表格中的数据补全y关于x的函数图象;
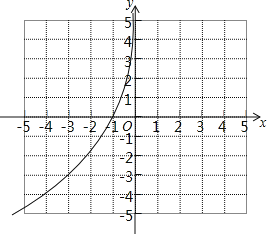
(3)结合函数图象,解决下列问题:
①写出函数y的一条性质:______;
②当函数值y≥![]() 时,x的取值范围是______;
时,x的取值范围是______;
③当函数值y=-x时,结合图象请估算x的值为______(结果保留一位小数)
【答案】(1)y=x-![]() (x≠0);(2)2
(x≠0);(2)2![]() ,3
,3![]() ;(3)①当x≥1时,y随x的增大而增大;②x=-
;(3)①当x≥1时,y随x的增大而增大;②x=-![]() 或x≥2;③±0.7
或x≥2;③±0.7
【解析】
(1)把(-1,0),(2,1![]() )代入y=k1x+
)代入y=k1x+![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)当x=3时,当x=4时,定义函数解析式即可得到结论;补全y关于x的函数图象即可;
(3)根据函数图象即可得到结论.
解:(1)把(-1,0),(2,1![]() )代入y=k1x+
)代入y=k1x+![]() 得,
得,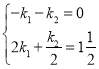 ,
,
解得: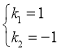 ,
,
∴y与x的函数表达式为:y=x-![]() (x≠0);
(x≠0);
故答案为:y=x-![]() (x≠0);
(x≠0);
(2)当x=3时,m=3-![]() =2
=2![]() ,当x=4时,n=4-
,当x=4时,n=4-![]() =3
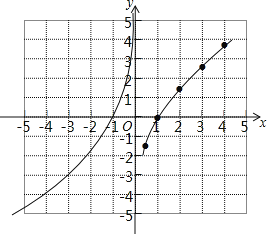
=3![]() ;补全y关于x的函数图象如图所示;
;补全y关于x的函数图象如图所示;
故答案为:2![]() ,3
,3![]() ;
;
(3)由图象知,①当x≥1时,y随x的增大而增大;
②当函数值y≥![]() 时,x的取值范围是:x=-
时,x的取值范围是:x=-![]() 或x≥2;
或x≥2;
③当函数值y=-x时,结合图象请估算x的值为±0.7,
故答案为:当x≥1时,y随x的增大而增大;x=-![]() 或x≥2;±0.7.
或x≥2;±0.7.

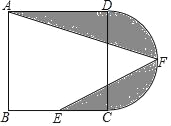
【题目】如图1,线段AB及一定点C、P是线段AB上一动点,作直线CP,过点A作AQ⊥CP于点Q,已知AB=7cm,设A、P两点间的距离为xcm,A、Q两点间的距离为y1cm,P、Q两点间的距离为y2cm.小明根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
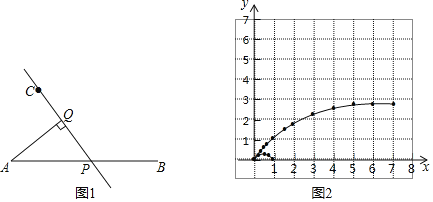
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值.
x/cm | 0 | 0.3 | 0.5 | 0.8 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 |
y1/cm | 0 | 0.28 | 0.49 | 0.79 | 1 | 1.48 | 1.87 | 2.37 | 2.61 | 2.72 | 2.76 | 2.78 |
y2/cm | 0 | 0.08 | 0.09 | 0.06 | 0 | 0.29 | 0.73 | 1.82 |
| 4.20 | 5.33 | 6.41 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△APQ中有一个角为30°时,AP的长度约为 cm.