题目内容
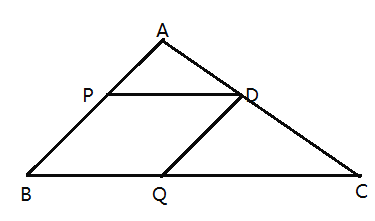
【题目】如图,已知抛物线![]() 经过点
经过点![]() 、
、![]() 和
和![]() ,
,![]() 垂直于
垂直于![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,
,![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 是该抛物线的对称轴,点
是该抛物线的对称轴,点![]() 是抛物线的顶点.
是抛物线的顶点.

(1)求出该二次函数的表达式及点![]() 的坐标;
的坐标;
(2)若![]() 沿
沿![]() 轴向右平移,使其直角边
轴向右平移,使其直角边![]() 与对称轴
与对称轴![]() 重合,再沿对称轴
重合,再沿对称轴![]() 向上平移到点
向上平移到点![]() 与点
与点![]() 重合,得到
重合,得到![]() ,求此时
,求此时![]() 与矩形
与矩形![]() 重叠部分图形的面积;
重叠部分图形的面积;
(3)若![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位长度(
个单位长度(![]() )得到
)得到![]() ,
,![]() 与
与![]() 重叠部分图形的面积记为
重叠部分图形的面积记为![]() ,求
,求![]() 与
与![]() 之间的函数表达式,并写出自变量
之间的函数表达式,并写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)抛物线的解析式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)
;(2) ![]() ; (3)
; (3) 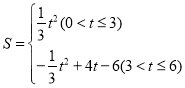 .
.
【解析】
(1)将点A(-3,0)、B(9,0)和C(0,4)代入y=ax2+bx+c即可求出该二次函数表达式,因为CD垂直于y轴,所以令y=4,求出x的值,即可写出点D坐标;
(2)设A1F交CD于点G,O1F交CD于点H,求出顶点坐标,证△FGH∽△FA1O1,求出GH的长,因为Rt△A1O1F与矩形OCDE重叠部分的图形是梯形A1O1HG,所以S重叠部分=![]() -S△FGH,即可求出结果;
-S△FGH,即可求出结果;
(3)当0<t≤3时,设O2C2交OD于点M,证△OO2M∽△OED,求出O2M=![]() t,可直接求出S=
t,可直接求出S=![]() =
=![]() OO2×O2M=
OO2×O2M=![]() t2;当3<t≤6时,设A2C2交OD于点M,O2C2交OD于点N,分别求出直线OD与直线A2C2的解析式,再求出其交点M的坐标,证△DC2N∽△DCO,求出C2N=
t2;当3<t≤6时,设A2C2交OD于点M,O2C2交OD于点N,分别求出直线OD与直线A2C2的解析式,再求出其交点M的坐标,证△DC2N∽△DCO,求出C2N=![]() (6-t),由S=S四边形A2Q2NM=
(6-t),由S=S四边形A2Q2NM=![]() ,可求出S与t的函数表达式.
,可求出S与t的函数表达式.
(1)∵抛抛线![]() 经过点
经过点![]() 、
、![]() 和
和![]() ,
,
∴抛物线的解析式为![]() ,
,
∵点![]() 在抛物线上,
在抛物线上,
∴![]() ,
,
∴![]() ,
,
∴抛物线的解析式为:![]() ,
,
∵![]() 垂直于
垂直于![]() 轴,
轴,![]() ,
,
令![]() ,
,
解得,![]() 或
或![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
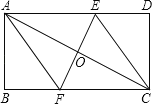
(2)如图1所示,设![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,
∵点![]() 是抛物线
是抛物线![]() 的顶点,
的顶点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴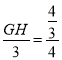 ,
,
解得,![]() ,
,
∵![]() 与矩形
与矩形![]() 重叠部分的图形是梯形
重叠部分的图形是梯形![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
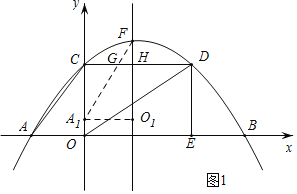
(3)①当![]() 时,如图2所示,设
时,如图2所示,设![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
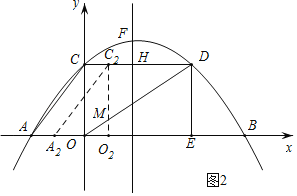
②当![]() 时,如图3所示,设
时,如图3所示,设![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,
将点![]() 代入
代入![]() ,
,
得,![]() ,
,
∴![]() ,
,
将点![]() ,
,![]() 代入
代入![]() ,
,
得,![]() ,
,
解得,![]() ,
,![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
联立![]() 与
与![]() ,
,
得,![]() ,
,
解得,![]() ,
,
∴两直线交点![]() 坐标为
坐标为![]() ,
,
故点![]() 到
到![]() 2的距离为
2的距离为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
∴![]() 与
与![]() 的函数关系式为:
的函数关系式为: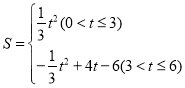 .
.

【题目】一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.