题目内容
【题目】如图，AB是半圆O的直径，且AB=12，点C为半圆上的一点．将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是（ ）
A. 4πB. 5πC. 6πD. 8π
【答案】C
【解析】
过点O作OD⊥BC于点D,交弧BC于点E,则可判断点O是弧BC的中点,由折叠的性质可得OD=
OE=R=3,在Rt△OBD中求出∠OBD=30°,继而得出∠AOC,求出扇形AOC的面积即可得出阴影部分的面积
过点O作0D⊥BC于点
D,交弧BC于点E,连接OC
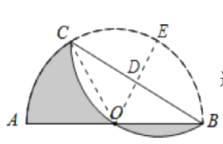
则点E是弧BEC的中点,由折叠的性质可得点O为弧BOC的中点,
∴S弓形BO=S弓形CO，
在Rt△BOD中,OD=DE=R=3,OB=R=6
∴∠OBD=30°
∴∠AOC=60°
∴S月影=S扇形AOC=
故选:C
练习册系列答案
应用题作业本系列答案
相关题目
