题目内容
【题目】已知∠AOB=30°,其平分线是OD,自O点引射线OC,若∠AOC:∠COB=2:3,则∠COD=__________.
【答案】3°或75°
【解析】
由于自O点引射线OC位置没有确定,需要分情况来求.由于∠AOC:∠COB=2:3,∠AOB=30°,可以求得∠AOC的度数,OD是角平分线,可以求得∠AOD的度数,∠COD=∠AOD-∠AOC或∠COD=∠AOD+∠AOC即可.
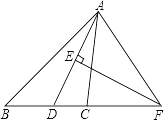
解:若OC在∠AOB内部, 如图1,∠AOC∶∠COB=2∶3,设∠AOC=2x,∠COB=3x
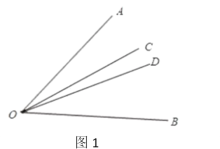
∵∠AOB=30°,
∴2x+3x=30°
解得x=6°
∴∠AOC=2x=2×6°=12°,∠COB=3x=3×6°=18°
∵OD平分∠AOB,∴∠AOD=15°
∴∠COD=∠AOD-∠AOC=15°-12°=3°
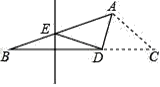
若OC在∠AOB外部,如图2
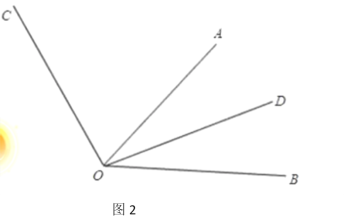
∵∠AOC∶∠COB=2∶3,设∠AOC=2x,∠COB=3x
∵∠AOB=30°
3x-2x=30°
得x=30°
∴∠AOC=2x=2×30°=60°,∠COB=3x=3×30°=90°,
∵OD平分∠AOB,
∴∠AOD=15°
∴∠COD=∠AOC+∠AOD=60°+15°=75°,
故OC与∠AOB的平分线所成的角的度数为3°或75°.

【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆,但由于种种原因,实际每天的销售量与计划量相比有出入。下表是某周的销售情况(超额记为正、不足记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
(1)根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。
(3)该店实行每日计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖15元;少销售一辆扣20元,那么该店铺的销售人员这一周的工资总额是多少元?