题目内容
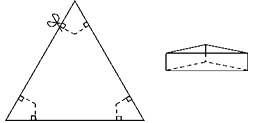
【题目】如图，在△ABC 中，∠BAC=120°，点 D 是 BC 上一点，BD 的垂直平分线交 AB 于点E，将△ACD 沿 AD 折叠，点 C 恰好与点 E 重合，则∠B 等于_______°；
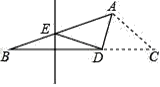
【答案】20
【解析】
根据折叠的性质得出∠C=∠AED，再利用线段垂直平分线的性质得出BE=DE，进而得出∠B=∠EDB，进而得出∠C=2∠B，利用三角形内角和解答即可．
∵将△ACD沿AD折叠，点C恰好与点E重合，
∴∠C=∠AED，
∵BD的垂直平分线交AB于点E，
∴BE=DE，
∴∠B=∠EDB，
∴∠C=∠AED=∠B+∠EDB=2∠B，
在△ABC中，∠B+∠C+∠BAC=∠B+2∠B+120°=180°，
解得：∠B=20°，
故答案为20
练习册系列答案
相关题目
【题目】股民李金上星期六买进某公司的股票，每股
元，下表为本周内该股票的涨跌情况：
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌(与前一天相比) |
|
|
|
|
|
|
星期三收盘时，每股是________元；本周内最高价是每股________元， 最低价是每股______元．
