题目内容
【题目】如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为 . 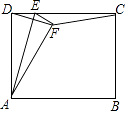
【答案】![]() 或
或 ![]() 或6
或6
【解析】解:分三种情况:①如图,当DF=CF时,△DFC是等腰三角形,
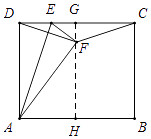
过F作FG⊥CD于G,交AB于H,则FH⊥AB,
∵DG= ![]() CD=AH=3,AF=AD=5,
CD=AH=3,AF=AD=5,
∴Rt△AFH中,HF=4,
∴GF=GH﹣FH=1,
设DE=FE=x,则EG=3﹣x,
∵Rt△EFG中,(3﹣x)2+12=x2,
解得x= ![]() ,
,
∴DE的长为 ![]() ;②如图,当DC=DF=6时,△DFC是等腰三角形,
;②如图,当DC=DF=6时,△DFC是等腰三角形,
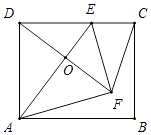
由折叠可得,AE⊥DF,DO= ![]() DF=3,
DF=3,
∴Rt△AOD中,AO=4,
∵∠ADE=90°,
∴∠ODE=∠OAD,
又∵∠DOE=∠AO90°,
∴△DOE∽△AOD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得DE= ![]() ;③如图,当DC=FC时,△DFC是等腰三角形,
;③如图,当DC=FC时,△DFC是等腰三角形,
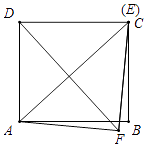
∴点C在DF的垂直平分线上,
又∵AE垂直平分DF,
∴点E与点C重合,
∴DE=DC=6,
综上所述,DE的长为 ![]() 或
或 ![]() 或6.
或6.
所以答案是: ![]() 或
或 ![]() 或6.
或6.
【考点精析】掌握等腰三角形的性质和矩形的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目