题目内容
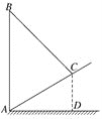
【题目】如图,是斜坡AC上的一根电线杆AB用钢丝绳BC进行固定的平面图.已知斜坡AC的长度为4 m,钢丝绳BC的长度为5 m,AB⊥AD于点A,CD⊥AD于点D,若CD=2 m,则电线杆AB的高度是多少.(结果保留根号)
【答案】2+![]()
【解析】
过点C作CE∥AD交AB于点E,得到矩形ADCE,那么AE=CD=2,CE=AD.先在直角△ACD中利用勾股定理求出AD,然后在直角△BCE中利用勾股定理求出BE,那么AB=AE+BE,问题得解.
解 过点C作CE∥AD交AB于点E,
∵AB⊥AD于点A,CD⊥AD于点D,
∴四边形ADCE是矩形,
∴AE=CD=2,CE=AD.
在直角△ACD中,
∵∠ADC=90°,
∴AD=![]() =2
=2![]() ,
,
∴CE=AD=2![]() .
.
在直角△BCE中,∵∠BEC=90°,
∴BE=![]() =
=![]() ,
,
∴AB=AE+BE=2+![]() .
.
即电线杆AB的高度是(2+![]() )m.
)m.
故答案为:2+![]() .
.


练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目