题目内容
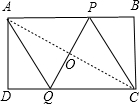
如图,矩形ABCD中,AB=CD=x,AD=BC=y,把它折叠起来,使顶点A与C重合,则折痕PQ的长度为( )
A.
| B.
| C.
| D.
|

∵A,C两点关于PQ对称,所以AO=CO,
∵AC⊥QP,从而∠AOP=∠QOC=90°,
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠APQ=∠PQC.
∴△APO≌△CQO,
∴CQ=AP,
由PQ⊥AC且平分AC,可知AQ=CQ.
∴四边形AQCP是菱形,
设AP=a,则AQ=a,DQ=x-a,
在Rt△ADQ中,利用勾股定理可知:a2=y2+(x-a)2,
∴整理得:2ax=x2+y2,
解得a=
,
菱形AQCP的面积为:
PQ•AC=CQ•AD,
∴
PQ×
=
×y,
整理得:PQ×
=
×y,
解得:PQ=
.
故选:A.
∵AC⊥QP,从而∠AOP=∠QOC=90°,
∵四边形ABCD是矩形,
∴AB∥DC,
∴∠APQ=∠PQC.
∴△APO≌△CQO,
∴CQ=AP,
由PQ⊥AC且平分AC,可知AQ=CQ.
∴四边形AQCP是菱形,
设AP=a,则AQ=a,DQ=x-a,
在Rt△ADQ中,利用勾股定理可知:a2=y2+(x-a)2,
∴整理得:2ax=x2+y2,
解得a=
| x2+y2 |
| 2x |
菱形AQCP的面积为:
| 1 |
| 2 |
∴
| 1 |
| 2 |
| x2+y2 |
| x2+y2 |
| 2x |
整理得:PQ×
| x2+y2 |
| x2+y2 |
| x |
解得:PQ=
| y |
| x |
| x2+y2 |
故选:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
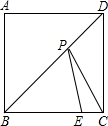




 一个梯形教具,现进行如下操作:
一个梯形教具,现进行如下操作:



