Question

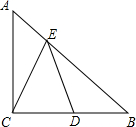
如图，已知，在Rt△ABC中，∠C=90°，沿过B点的一条直线BE折叠这个三角形，使C点与AB边上的一点D重合．
（1）当∠A满足什么条件时，点D恰为AB的中点写出一个你认为适当的条件，并利用此条件证明D为AB的中点；
（2）在（1）的条件下，若DE=1，求△ABC的面积．

Answer 1

（1）添加条件是∠A=30°．
证明：∵∠A=30°，∠C=90°，所以∠CBA=60°，
∵C点折叠后与AB边上的一点D重合，
∴BE平分∠CBD，∠BDE=90°，
∴∠EBD=30°，
∴∠EBD=∠EAB，所以EB=EA；
∵ED为△EAB的高线，所以ED也是等腰△EBA的中线，
∴D为AB中点．

（2）∵DE=1，ED⊥AB，∠A=30°，∴AE=2．
在Rt△ADE中，根据勾股定理，得AD=

22-1

=

3

，
∴AB=2

3

，∵∠A=30°，∠C=90°，
∴BC=

1

2

AB=

3

．
在Rt△ABC中，AC=

AB2-BC2

=3，
∴S_△ABC=

1

2

×AC×BC=

3 3

2

．