题目内容
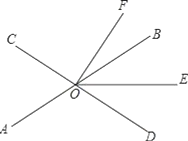
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
【答案】(1)55°;(2)①∠FOE=![]() x;②100°.
x;②100°.
【解析】试题分析:(1)、根据对顶角的性质得出∠BOD的度数,根据直角和角平分线的性质求出∠BOF和∠BOE的度数,从而根据∠EOF=∠BOF+∠BOD得出答案;(2)、根据角平分线的性质得出∠BOE=∠DOE,根据平角的性质得出∠COE=∠AOE,最后根据角平分线的性质得出∠FOE的度数;根据题意得出∠BOE= ![]() -15°,根据∠BOE+∠AOE=180°求出x的值,最后根据∠AOC=2∠BOE得出答案.
-15°,根据∠BOE+∠AOE=180°求出x的值,最后根据∠AOC=2∠BOE得出答案.
试题解析:解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF﹣∠BOD,∴∠FOB=90°﹣70°=20°,
∵OE平分∠BOD,∴∠BOE=![]() ∠BOD=
∠BOD=![]() ×70°=35°,
×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°,
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x,
∵OF平分∠COE, ∴∠FOE=![]() x;
x;
②∵∠BOE=∠FOE﹣∠FOB,∴∠BOE=![]() x﹣15°,
x﹣15°,
∵∠BOE+∠AOE=180°,∴![]() x ﹣15°+x=180°,解得:x=130°,
x ﹣15°+x=180°,解得:x=130°,
∴∠AOC=2∠BOE=2×(180°﹣130°)=100°.

练习册系列答案
相关题目