题目内容
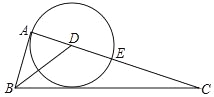
【题目】已知:在等腰直角三角形ABC中,AB=BC,∠ABC=90°.D是平面上一点,连结BD.将线段BD绕点B逆时针旋转90°得到线段BE,连结AE,CD.
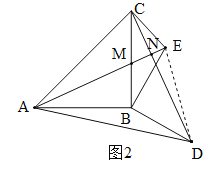
(1)在图1中补全图形,并证明:AE⊥CD.
(2)当点D在平面上运动时,请猜测线段AD,CE,AB,BD之间的数量关系.
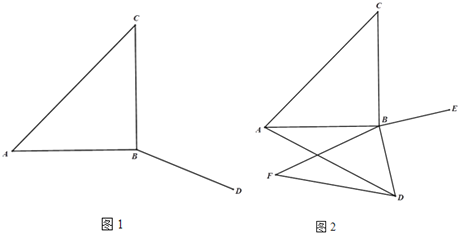
(3)如图2,作点A关于直线BE的对称点F,连结AD,DF,BF.若AB=11,BD=7,AD=14,求线段DF的长度.
【答案】(1)详见解析;(2)![]() ;(3)DF=12
;(3)DF=12
【解析】
(1)由旋转的性质得到∠DBE=90°,BD=BE,进而可得∠ABE=∠CBD,即可证明△ABE≌△CBD,由全等三角形对应角相等得到∠EAB=∠DCB.在△AMB和△CMN,根据对顶角相等和三角形内角和定理即可得到∠CNM=90°,即可得出结论;
(2)连接ED.在Rt△CNE、Rt△AND、Rt△ANC、Rt△DNE中,分别利用勾股定理即可得出结论.
(3)延长EB到G.由A和F关于直线BE对称,得到∠ABG=∠FBG,AB=BF,进而得到BC=BF.根据邓娇的余角相等得到∠CBE=∠FBD,即可证明△CBE≌△FBD,根据全等三角形对应边相等得到CE=FD.由(2)的结论可求出CE的长,等量代换即可得出结论.
(1)作图见图1.
∵将线段BD绕点B逆时针旋转90° 得到线段BE,
∴∠DBE=90°,BD=BE.
∵∠ABC=90°,
∴∠ABE=∠CBD.
在△ABE和△CBD中,∵AB=BC,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD,
∴∠EAB=∠DCB.
∵∠AMB=∠CMN,
∴∠CNM=∠ABM=90°,
∴AE⊥CD;
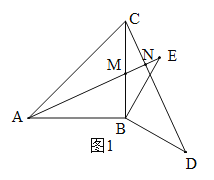
(2)![]() .理由如下:
.理由如下:
连接ED,如图2.
∵AE⊥CD,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
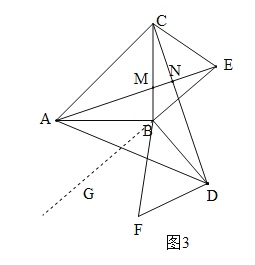
(3)延长EB到G,如图3.
∵A和F关于直线BE对称,
∴∠ABG=∠FBG,AB=BF.
∵AB=BC,
∴BC=BF.
∵∠ABC=∠DBE=90°,
∴∠ABG+∠CBE=90°,∠FBG+∠FBD=90°,
∴∠CBE=∠FBD.
在△CBE和△FBD中,∵CB=FB,∠CBE=∠FBD,BE=BD,
∴△CBE≌△FBD,
∴CE=FD.
由(2)可知:![]() ,
,
∴![]() ,
,
∴CE=12,
∴DF=CE=12.

【题目】某数学兴趣小组根据学习函数的经验,对分段函数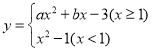 的图象与性质进行了探究,请补充完整以下的探究过程.
的图象与性质进行了探究,请补充完整以下的探究过程.
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | -1 | 0 | 1 | 0 | -3 | … |
(1)填空:a= .b= .
(2)①根据上述表格数据补全函数图象;
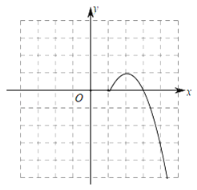
②该函数图象是轴对称图形还是中心对称图形?
(3)若直线![]() 与该函数图象有三个交点,求t的取值范围.
与该函数图象有三个交点,求t的取值范围.