题目内容
【题目】如图,建筑物AB的高为6cm,在其正东方向有个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A、塔项C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() =1.73,精确到0.1m)
=1.73,精确到0.1m)

【答案】通信塔CD的高度约为15.9cm.
【解析】
过点A作AE⊥CD于E,设CE=xm,解直角三角形求出AE,解直角三角形求出BM、DM,即可得出关于x的方程,求出方程的解即可.
过点A作AE⊥CD于E,
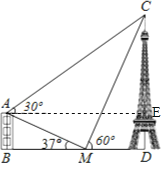
则四边形ABDE是矩形,
设CE=xcm,
在Rt△AEC中,∠AEC=90°,∠CAE=30°,
所以AE=![]() xcm,
xcm,
在Rt△CDM中,CD=CE+DE=CE+AB=(x+6)cm,
DM=![]() cm,
cm,
在Rt△ABM中,BM=![]() cm,
cm,
∵AE=BD,
∴![]() ,
,
解得:x=![]() +3,
+3,
∴CD=CE+ED=![]() +9≈15.9(cm),
+9≈15.9(cm),
答:通信塔CD的高度约为15.9cm.

练习册系列答案
相关题目