题目内容
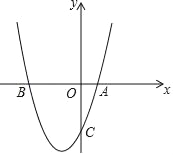
【题目】如图,抛物线y=x2﹣2mx+3m与x轴交于A、B两点,与y轴交于点C(0,﹣3)
(1)求该抛物线的解析式;
(2)点D为该抛物线上的一点、且在第二象限内,连接AC,若∠DAB=∠ACO,求点D的坐标;
(3)若点E为线段OC上一动点,试求2AE+![]() EC的最小值.
EC的最小值.
【答案】(1)y=x2+2x﹣3;(2)点D的坐标为(﹣![]() ,
,![]() );(3)4
);(3)4![]() .
.
【解析】
(1)把点C的坐标代入抛物线求出m,即可求出解析式;
(2)过D点作x轴的垂线,交x轴于点H,点D的坐标为(n,n 2+2 n﹣3),易知∠DAB =∠ACO ,利用tan∠DAB=tan∠ACO即可求得n的值,即可求出D点坐标;
(3)根据B,C坐标求出直线BC的解析式为y=-x-3,故∠BCO=45°,则EF=![]() EC,AE+
EC,AE+![]() EC=AE+EF,故当A、E、F三点共线时,AE+
EC=AE+EF,故当A、E、F三点共线时,AE+![]() EC最小,即2AE+
EC最小,即2AE+![]() EC最小,
EC最小,
根据BC⊥AF可设直线AF的表达式为:y=x+b,代入A点即可求出直线AF,令x=0,可求出E点坐标,即可求出此时2AE+![]() EC的值.
EC的值.
解:(1)把点C的坐标代入抛物线表达式得:9+6m+3m=0,
解得:m=﹣1,
故该抛物线的解析式为:y=x2+2x﹣3;
(2)过D点作x轴的垂线,交x轴于点H,过点E作EF⊥BC,交BC于点F,
令y=0,求得A(1,0),B(-3,0).
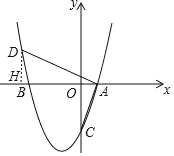
设:点D的坐标为(n,n 2+2n﹣3),
∵∠DAB=∠ACO,
∴tan∠DAB=tan∠ACO,
即:![]() =
=![]() ,
,![]() =
=![]() ,
,
解得:![]() =
=![]() 或1(舍去m=1),
或1(舍去m=1),
故点D的坐标为(![]() ,
,![]() );
);
(3)根据B,C坐标求出直线BC的解析式为y=-x-3,
过点E作EF⊥BC,交BC于点F,
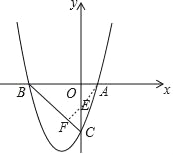
则EF=![]() EC,AE+
EC,AE+![]() EC=AE+EF,
EC=AE+EF,
∴当A、E、F三点共线时,AE+![]() EC最小,即2AE+
EC最小,即2AE+![]() EC最小,
EC最小,
设:直线AF的表达式为:y=x+b,
将点A坐标(1,0)代入上式,1+b=0,则b=﹣1,
则直线AE的表达式为:y=x﹣1,则点E的坐标为(0,﹣1),
则EC=3﹣1=2,AE=![]()
2AE+![]() EC=2
EC=2![]() +2
+2![]() =4
=4![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案