题目内容
【题目】如图,四边形ABCD是正方形,点E、K分别在BC、AB上,CE=BK,点G在BA的延盖
长线上,且DG⊥DE.
(1)如图(1)求证:CK=DG;
(2)如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等
的三角形。
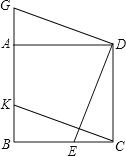
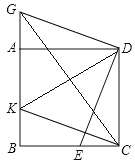
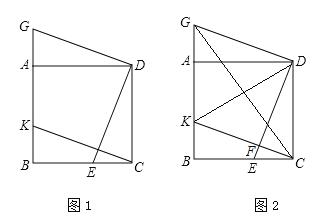
图1 图2
【答案】(1)证明见解析;(2)ΔGKD,ΔCKD,ΔKGC,ΔDGC.
【解析】试题分析:(1)依据正方形的性质,判定△DCE≌△CBK,即可得到DE=CK,再判定△ADG≌△CDE,即可得到DG=DE,进而得出DG=CK;
(2)依据△DCE≌△CBK,可得S△DCE=S△BCK,进而得到S四边形BEFK=S△CDF,进而得出S四边形BEDK=S△CDK,再根据四边形CDGK是平行四边形,即可得到S△CDK=S△CDG=S△GDK=S△CGK.
试题解析:解:(1)如图1.∵四边形ABCD是正方形,∴DC=CB=AD,∠B=∠DCE=∠DAG=90°.∵CE=BK,∴△DCE≌△CBK,∴DE=CK.∵DG⊥DE,∴∠ADG+∠ADE=90°=∠CDE+∠ADE,∴∠ADG=∠CDE.又∵∠DAG=∠DCE=90°,AD=CD,∴△ADG≌△CDE,∴DG=DE,∴DG=CK;
(2)如图2.∵△DCE≌△CBK,∴S△DCE=S△BCK,∴S四边形BEFK=S△CDF,∴S四边形BEFK+S△DFK=S△CDF+S△DFK,即S四边形BEDK=S△CDK.∵△ADG≌△CDE,∴CE=BK=AG,∴CD=AB=GK.又∵DG=CK,∴四边形CDGK是平行四边形,∴S△CDK=S△CDG=S△GDK=S△CGK,∴与四边形BEDK面积相等的三角形为△CDK,△CDG,△GDK,△GCK.

练习册系列答案
相关题目







