题目内容
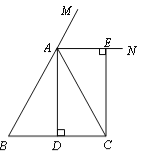
【题目】已知:如图,CD、C′D′分别是Rt△ABC,Rt△A′B′C′斜边上的高,且CB=C′B′,CD=C′D′.求证:△ABC≌△A′B′C′.


【答案】见解析
【解析】分析:欲证△ABC≌△A′B′C′,根据已知条件,已经有∠ACB=∠A′C′B′=90°,CB=C′B′,即已知一边一角,由三角形全等的判定定理可知,还需有一对角相等或者边AC=A′C′.而根据已知条件CB=C′B′,CD=C′D′,易证Rt△CDB≌Rt△C′D′B′,得出∠B=∠B′,从而根据ASA证明出△ABC≌△A′B′C′.
详解:
证明:∵CD⊥AB,C'D'⊥A'B' (已知)
∴∠CDB=∠C'D'B'=90°.(垂直的意义)
在Rt△CDB和Rt△C'D'B'中,
CB=C'B',CD=C'D',(已知)
∴Rt△CDB≌Rt△C'D'B'(HL),
∴∠B=∠B',(全等三角形的对应角相等)
∵△ABC,△A'B'C'都是直角三角形 (已知)
∴∠ACB=∠A'C'B'=90°(直角三角形的意义)
在△ABC和△A'B'C'中,
∠B=∠B'
CD=C'D'
∠ACB=∠A'B'C'
∴△ABC≌△A'B'C'(ASA)

练习册系列答案
相关题目