题目内容
【题目】(10分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.
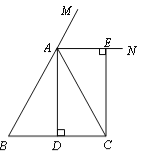
【答案】四边形ADCE是矩形.理由见解析.
【解析】
试题分析:因为AD⊥BC,CE⊥AN,所以∠ADC=∠CEA=90°,然后根据互补和角平分线证明∠DAE=90°即可.
试题解析:四边形ADCE是矩形.
证明:因为AB=AC,AD⊥BC,所以∠BAD=∠CAD(三线合一),
又因为AN平分∠CAM,∠BAC+∠CAM=180°,所以∠CAD+∠CAN=180°/2=90°,
又因为CE⊥AN,
所以AD∥CE,∠ADC=∠CEA=∠DAE=90°,则∠DCE=90°,
所以四边形ADCE是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目