题目内容
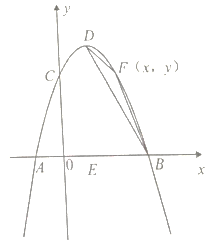
【题目】平面直角坐标系中，点A是
轴正半轴上一个定点，点P是函数
（＞0）上一个动点，PB⊥
轴于点B，连结PA,当点P的横坐标逐渐增大时，四边形OAPB的面积将会（ ）
A. 逐渐增大 B. 先增后减 C. 逐渐减小 D. 先减后增
【答案】C
【解析】根据题意画出图形，设出点P的坐标，得到PB、OB的长，然后根据梯形的面积得到四边形AOPB的面积关系，根据OA是定值和函数的关系得解.
根据题意画出图形为：
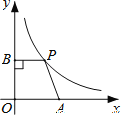
设点P的坐标为（x，
），
∴PB=x，OB=
∴四边形AOPB的面积=
×（PB+OA）×OB=×PB×OB+×OA×OB=2+
∵AO是定值，
∴四边形OAPB的面积是个减函数，即点P的横坐标逐渐增大时四边形OAPB的面积逐渐减小．
故选：C.
练习册系列答案
相关题目
【题目】某学校计划在总费用2300元的限额内，租用客车送234名学生和6名教师集体外出活动，每辆客车上至少要有1名教师.现有甲、乙两种大客车，它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
