ЬтФПФкШн
ЁОЬтФПЁПНЋвЛОиаЮжНЦЌOABCЗХдкЦНУцжБНЧзјБъЯЕжаЃЌOЃЈ0ЃЌ0ЃЉЃЌAЃЈ6ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЃЎЖЏЕуQДгЕуOГіЗЂвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШбиOCЯђжеЕуCдЫЖЏЃЌдЫЖЏ![]() УыЪБЃЌЖЏЕуPДгЕуAГіЗЂвдЯрЕШЕФЫйЖШбиAOЯђжеЕуOдЫЖЏЃЎЕБЦфжавЛЕуЕНДяжеЕуЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЈУыЃЉЃЎ
УыЪБЃЌЖЏЕуPДгЕуAГіЗЂвдЯрЕШЕФЫйЖШбиAOЯђжеЕуOдЫЖЏЃЎЕБЦфжавЛЕуЕНДяжеЕуЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЈУыЃЉЃЎ
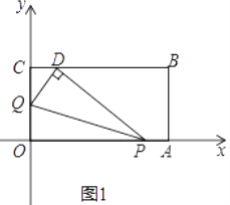
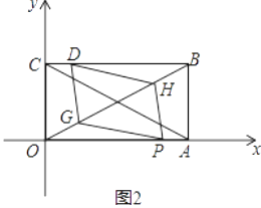
ЃЈ1ЃЉЧѓЕуBЕФзјБъЃЌВЂгУКЌtЕФДњЪ§ЪНБэЪОOPЃЌOQЃЛ
ЃЈ2ЃЉЕБt=1ЪБЃЌШчЭМ1ЃЌНЋЁїOPQбиPQЗелЃЌЕуOЧЁКУТфдкCBБпЩЯЕФЕуDДІЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌОиаЮЖдНЧЯпACЃЌBOНЛгкMЃЌШЁOMжаЕуGЃЌBMжаЕуHЃЌЧѓжЄЃКЕБt=1ЪБЫФБпаЮDGPHЪЧЦНааЫФБпаЮЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЈ6ЃЌ3ЃЉЃЌOQ=![]() +tЃЌ OP= 6ЉtЃЛЃЈ2ЃЉDЃЈ1ЃЌ3ЃЉЃЛЃЈ3ЃЉжЄУїМћНтЮі.
+tЃЌ OP= 6ЉtЃЛЃЈ2ЃЉDЃЈ1ЃЌ3ЃЉЃЛЃЈ3ЃЉжЄУїМћНтЮі.
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉИљОнОиаЮЕФаджЪЧѓГіЕуBЕФзјБъЃЌИљОнЖЏЕуЮЪЬтЧѓГіOPКЭOQЕФГЄЖШЃЛЃЈ2ЃЉИљОнелЕўЭМаЮЕФаджЪЧѓГіOQКЭDQЕФГЄЖШЃЌШЛКѓИљОнЙДЙЩЖЈРэЧѓГіCDЕФГЄЖШЃЌЕУЕНЕуDЕФзјБъЃЛЃЈ3ЃЉИљОнвЛзщЖдБпЦНааЧвЯрЕШЕФЫФБпаЮЮЊЦНааЫФБпаЮНјааХаЖЈЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉBЃЈ6,3ЃЉЃЛOP="OA-AP=6-t," OQ=![]() +tЃЎ
+tЃЎ
ЃЈ2ЃЉЕБt=1ЪБЃЌOP=5ЃЌOQ=![]() ,дђCQ=3-
,дђCQ=3-![]() =
=![]() ЃЌ
ЃЌ
гЩелЕўПЩжЊЃКЁїOPQЁеЁїDPQ,
ЁрOQ=DQ=![]()
гЩЙДЙЩЖЈРэ,ЕУЃКCD=1
ЁрDЃЈ1,3ЃЉ
ЃЈ3ЃЉЁпЫФБпаЮOABCЪЧОиаЮЃЌ
ЁрOA=BC,
гжЁпCD=AP=1ЃЌ
ЁрBC-CD=OA-AP,МДBD=OP,
ЁпOM=MB,GЮЊOMжаЕуЃЌHЮЊBMжаЕу ,
ЁрOG="BH,"
ЁпOAЁЮBC
ЁрЁЯ1=ЁЯ2
дкЁїPOGКЭЁїDBHжаЃЌOG=BHЃЌЁЯ1=ЁЯ2ЃЌOP=DB
ЁрЁїPOGЁеЁїDBH
ЁрЁЯOGP=ЁЯBHDЃЌPG=DH
ЁрЁЯMGP=ЁЯDHM
ЁрPGЁЮDH
гжЁпPG=DH
ЁрЫФБпаЮDGPHЪЧЦНааЫФБпаЮЃЎ