题目内容
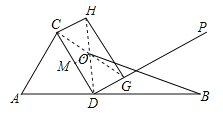
【题目】如图，线段AB的长为20，点D在AB上，△ACD是边长为8的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值为（ ）
A. 10 B. 6 C. 8
D. 6
【答案】A
【解析】解：如果，作射线MO⊥CD，则点M为CD的中点，由题意可得，点O为矩形CDGH的中点，所以无论G在射线DP上如何变化，O点的运动轨迹在CD的中垂线上，即O点在射线MO上．
∵DP⊥CD，∴MO∥DP，线段BO的最小值为B到射线MO的最小距离，所以当BO⊥DP时，BO取得最小值．
∵△ACD是边长为15的等边三角形，四边形CDGH是矩形，∴∠PDB=180°﹣60°﹣90°=30°，线段AB的长为20，∴BD=AB﹣AD=20-8=12，∴BO的最小值是：BDsin30°+
=12×
+4=10．故选A．
练习册系列答案
口算题天天练系列答案
相关题目
