题目内容
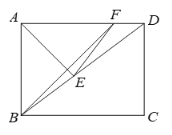
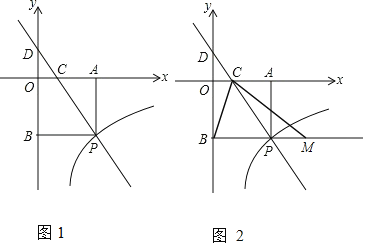
【题目】如图1,直线y1=kx+3与双曲线![]() (x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,
(x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,![]() .
.
(1)求OD和AP的长;
(2)求m的值;
(3)如图2,点M为直线BP上的一个动点,连接CB、CM,当△BCM为等腰三角形时,请直接写出点M的坐标.
【答案】(1)OD=3,AP=6;(2)m=4或9;(3)点M的坐标为(4,﹣6)或(10,﹣6)或(![]() ,﹣6)或(
,﹣6)或(![]() ,﹣6).
,﹣6).
【解析】
(1)设P(a,b),则OA=a,由![]() =
=![]() 得:C(
得:C(![]() a,0),由S△DBP=
a,0),由S△DBP=![]() ×DBBP=27,求出a值,进而求解;
×DBBP=27,求出a值,进而求解;
(2)将点P的坐标代入反比例解析式,即可求解;
(3)分BC=CM、BC=MB、MB=CM三种情况,分别求解即可.
解:(1)设P(a,b),则OA=a,
∵![]() =
=![]() ,
,
∴OC=![]() AC,
AC,
∴C(![]() a,0),
a,0),
∵点C在直线y=kx+3上,
∴0=![]() ak+3,即ka=﹣9,
ak+3,即ka=﹣9,
∴DB=3﹣b=3﹣(ka+3)=﹣ka=9,
∵BP=a,
∴S△DBP=![]() ×DBBP=27,
×DBBP=27,
∴![]() ×9a=27,
×9a=27,
∴a=6,
∴k=﹣![]() ,
,
∴一次函数的表达式为y=﹣![]() x+3;
x+3;
将x=6代入一次函数解析式得:y=﹣6,即P(6,﹣6),
∴AP=6,
由一次函数表达式得:点D(0,3),故OD=3;
(2)将点P的坐标代入反比例解析式得:m2﹣13m=﹣36,
解得:m=4或9;
(3)由(1)得,点Cspan>(2,0)、而点B(0,﹣6),设点M(m,﹣6);
则BC2=4+36=40,CM2=(m﹣2)2+36,MB2=m2,
当BC=CM时,40=(m﹣2)2+36,解得:m=4或0(舍去0);
当BC=MB时,同理可得:m=±![]() ;
;
当MB=CM时,同理可得:m=10,
故点M的坐标为(4,﹣6)或(10,﹣6)或(±![]() ,﹣6).
,﹣6).

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案