题目内容
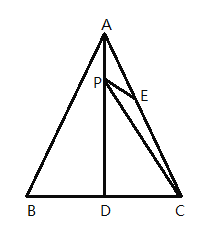
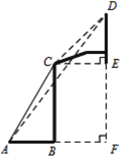
【题目】如图所示，一副篮架由配重、支架、篮板与篮筐组成，在立柱的C点观察篮板上沿D点的仰角为45°，在支架底端的A点观察篮板上沿D点的仰角为54°，点C与篮板下沿点E在同一水平线，若AB=1.91米，篮板高度DE为1.05米，求篮板下沿E点与地面的距离．（结果精确到0．1m，参考数据：sin54°≈0.80， cos54°≈0.60，tan54°≈1.33）
【答案】篮板下沿E点沿与地面的距离为2.9米．
【解析】
过D作DF⊥AB的延长线于F，连接CE，根据题目已知条件可以得到CE=DE=1.05，四边形CBFE为矩形，利用矩形的性质CE=BF=1.05，最后利用解直角三角形即可得出结果．
解：如图所示，过D作DF⊥AB的延长线于F，连接CE．
在Rt△DEC中，∠DCE=45°，DE=1.05（米），
∴CE=DE=1.05（米），
∵∠CBF=∠F=∠CEF=90°，
∴四边形CBFE为矩形，
∴CE=BF=1.05（米），
∴AF=AB+BF=2.96（米），
在Rt△AFD中，AF=2.96（米），∠DAF=54°，
由DF=AF·tan54°得DF≈3.94（米），
∴EF=3.94-1.05≈2.9（米）．
答：篮板下沿E点沿与地面的距离为2.9米．
轻松暑假总复习系列答案
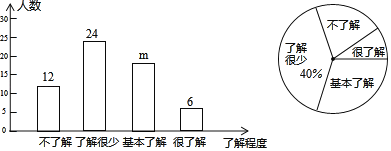
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心疾首．今年某校为确保学生安全，开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用
表示，共分成四组：
．
．
C．
D．
），下面给出了部分信息：
七年级10名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82
八年级10名学生的竞赛成绩在
组中的数据是：94，90，94
八年级抽取的学生竞赛成绩扇形统计图：
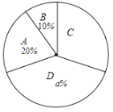
七、八年级抽取的学生竞赛成绩统计表：
年级 | 七年级 | 八年级 |
平均数 |
| 92 |
中位数 | 93 | 94 |
众数 | 99 | 100 |
方差 | 52 | 50.4 |
根据以上信息，解答下列问题：
（1）直接写出上述图表中
的值；
（2）根据以上数据，你认为该校七、八年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）；
（3）该校七、八年级共720人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（
）的学生人数是多少？
