Question

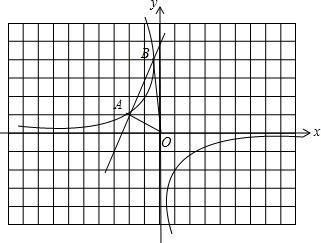
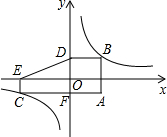
如图，过A（2，-1）分别作y轴、x轴的平行线交双曲线y=

k

x

于点B、点C，交两坐标轴于点G、F，过点C作CE⊥x轴于点E，过点B作BD⊥y轴于点D，连接ED，若四边形AGOF的面积等于△EOD的面积，则实数k=______．

Answer 1

∵反比例函数y=

k

x

的图象在一、三象限，
∴k＞0，
∵点A（2，-1），CE⊥x轴于点E，BD⊥y轴于点D，
∴B（2，

k

2

），C（-k，-1），S_矩形AGOF=2，
∴CF=k，DO=

k

2

，
∴S_△ODE=S_矩形AGOF=

1

2

×

k

2

×k=2，
解得k=2

2

或k=-2

2

（舍去）．
故答案为：2

2

．