题目内容
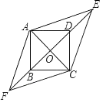
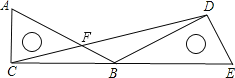
【题目】如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD.
(1)试判断△CBD的形状,并说明理由;
(2)求∠BDC的度数.
【答案】(1)△CBD是等腰三角形;(2)15°.
【解析】
(1)根据图形旋转不变性的性质得出△ABC≌△EBD,故可得出BC=BD,由此即可得出结论;
(2)根据图形选旋转不变性的性质求出∠EBD的度数,再由等腰三角形的性质即可得出∠BDC的度数.
(1)∵△EBD由△ABC旋转而成,
∴△ABC≌△EBD,
∴BC=BD,
∴△CBD是等腰三角形.
(2)∵△ABC≌△EBD,
∴∠EBD=∠ABC=30°,
∴∠DBC=180-30°=150°,
∵△CBD是等腰三角形,
∴∠BDC=![]() =
=![]() =15°.
=15°.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目