题目内容
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
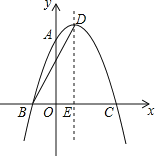
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
(3)点F在抛物线的对称轴上运动,是否存在点F,使△BFC的面积为4,如果存在,求出点F的坐标;如果不存在,请说明理由.
【答案】(1)y=-x2+2x+3;(2)2![]() ;(3)(1,2)或(1,-2).
;(3)(1,2)或(1,-2).
【解析】
(1)利用待定系数法求抛物线解析式;
(2)把(1)的解析式配成顶点式得到D点坐标,然后两点间的距离公式计算BD的长;
(3)先利用对称性确定C点坐标,设F(1,m),根据三角形面积公式得到![]() (3+1)|m|=4,然后解绝对值方程求出m即可得到点F的坐标.
(3+1)|m|=4,然后解绝对值方程求出m即可得到点F的坐标.
(1)把A(0,3),B(-1,0)代入y=ax2+2x+c得![]() ,即得
,即得![]() ,
,
∴抛物线的解析式为y=-x2+2x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴D(1,4),
∴BD=![]() =2
=2![]() ;
;
(3)存在.
∵抛物线的对称性为直线x=1,B(-1,0),
∴C(3,0),
设F(1,m),
∵△BFC的面积为4,
∴![]() (3+1)|m|=4,
(3+1)|m|=4,
∴|m|=2,解得m=2或m=-2,
∴点F的坐标为(1,2)或(1,-2).

练习册系列答案
相关题目
【题目】某服装店用4500元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价一进价),这两种服装的进价、标价如表所示
类型价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)请利用二元一次方程组求A,B两种新式服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?