题目内容
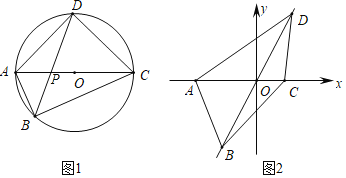
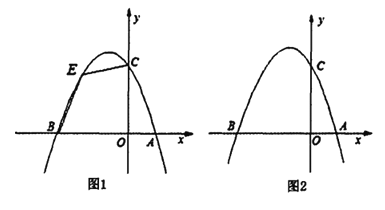
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(l)求抛物线的表达式;
(2)如图l,若点![]() 为第二象限抛物线上一动点,连接
为第二象限抛物线上一动点,连接![]() ,求四边形
,求四边形![]() 面积的最大值,并求此时
面积的最大值,并求此时![]() 点的坐标;
点的坐标;
(3)如图2,在![]() 轴上是否存在一点
轴上是否存在一点![]() 使得
使得![]() 为等腰三角形?若存在,请求出所有符合条件的点
为等腰三角形?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 最大值为
最大值为![]() ,点
,点![]() 坐标为
坐标为![]() ;(3)存在符合条件的点
;(3)存在符合条件的点![]() ,其坐标为
,其坐标为![]() 或
或![]() ,或
,或![]() 或
或![]()
【解析】
(1)将点A、B的坐标代入解析式即可得到答案;
(2)设![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,利用
,利用![]() 求出解析式即得到面积的最大值及点E的坐标;
求出解析式即得到面积的最大值及点E的坐标;
(3)存在,分以点C、A为顶点及线段AC为底边三种情况,分别求出点D的坐标即可.
解:(1)由题知:
![]() ,解得:
,解得:![]()
∴所求抛物线表达式为![]()
(2)过点![]() 作
作![]() 轴于点
轴于点![]()
设![]()
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
∴当![]() 时,
时,![]() 最大,且最大值为
最大,且最大值为![]() .
.
当![]() 时,
时,![]()
此时,点![]() 坐标为
坐标为![]()
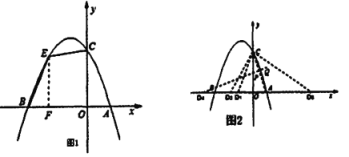
(3)连接![]()
①当点![]() 为顶点,
为顶点,![]() 时,此时
时,此时![]() 为底边的垂直平分线,
为底边的垂直平分线,
满足条件的点![]() ,与点
,与点![]() 关于
关于![]() 轴对称,
轴对称,
∴点![]() 坐标为
坐标为![]()
②当点![]() 为顶点,
为顶点,![]() 时,在
时,在![]() 中,
中,
∵![]() ,
,![]() ,由勾股定理得:
,由勾股定理得:![]() ,
,
以点![]() 为圆心,
为圆心,![]() 的长为半径作弧,交
的长为半径作弧,交![]() 轴于两点
轴于两点![]() ,即为满足条件的点,
,即为满足条件的点,
此时它们的坐标分别为![]() ,
,![]()
③当![]() 为底边时,线段
为底边时,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点
轴的交点![]() ,即为满足条件的点,
,即为满足条件的点,
设垂直![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,过
,过![]() 中点
中点![]() ,
,
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
![]() ,
, ,
,![]() ,
,
点![]() 的坐标为
的坐标为![]()
综上所述存在符合条件的点![]() ,其坐标为
,其坐标为![]() 或
或![]() ,或
,或![]() 或
或![]()

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目