��Ŀ����
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P(x,y)��������y���������x�IJ�y��x��ΪP��ġ���������ͼ��G�����е�ġ������е����ֵ��Ϊͼ��G�ġ�����ֵ��
(1)�ٵ�A(1,3) �ġ�����Ϊ ��
��������y=��x2+3x+3�ġ�����ֵ��Ϊ ��
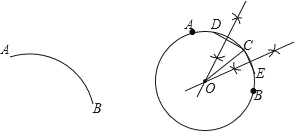
(2)ij���κ���y=��x2+bx+c(c��0) �ġ�����ֵ��Ϊ1����B(m,0)���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�ġ�������ȡ�
��ֱ��д��m= (�ú�c��ʽ�ӱ�ʾ)
����˶��κ����ı���ʽ��
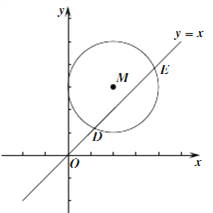
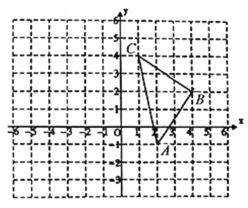
(3)��ͼ����ƽ��ֱ������ϵxOy�У���M(2,3)ΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��y=x�ཻ�ڵ�D��E��ֱ��д����M�ġ�����ֵ��Ϊ ��
���𰸡���1���� 2�� �� 4�� ��2���� m= ��c ; ��
![]() ����3��
����3��![]()
�����������������
��1���������������������Ķ��弴�ɵõ���A��1��3��������
���������Ķ���ɵ������κ���y=��x2+3x+3ͼ���ϵ�������Ϊ�� ![]() �����˹�ϵʽ�䷽�������y-x�����ֵ���Ӷ��õ�������y=��x2+3x+3�ġ�����ֵ����
�����˹�ϵʽ�䷽�������y-x�����ֵ���Ӷ��õ�������y=��x2+3x+3�ġ�����ֵ����
��2����������ɵ���0-m=c-0���ɴ˿ɵ���m=-c��
����m=-c�ɵõ�B������Ϊ��-c��0�����ѵ�B���������![]() �пɵ�
�пɵ�![]() ����
����![]() �ɵ�
�ɵ�![]() ����
����![]() ������
������![]() ������ֵΪ1�ɵã�
������ֵΪ1�ɵã� ![]() �������ɽ��b��c��ֵ���ɴ˼��ɵõ����κ����Ľ���ʽ��
�������ɽ��b��c��ֵ���ɴ˼��ɵõ����κ����Ľ���ʽ��
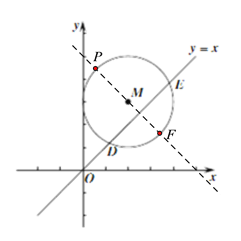
��3����ͼ������M��ֱ��PF��DE������M�ڵ�P��F������֪������ֱ��PF�Ľ���ʽΪy=-x+5����ֱ��y=x�ϵ����е�������Ϊ0��������ƽ������ֱ��y=x���Ҳ����ֱ��y=xԽԶ�ĵ�������Խ���֪����M�Ͼ���ֱ��y=x��Զ�ĵ��ǵ�P�����P������Ϊ��x��y���ɵ�P��M�ľ���Ϊ2���ɵõ�����x��y�ķ��̣���y=-x+5��ϼ��ɽ�õ�P�����꣬�����Ϳɵõ���M������ֵ��.
���������
��1���� ����A��������1��3����
����A���������3-1= 2��
�� �߶��κ����Ľ���ʽΪ��y=��x2+3x+3��
���ö��κ���ͼ�������е������������ ![]() ��
��
��![]() �����ö��κ���ͼ���ϵ�����������ֵΪ4��
�����ö��κ���ͼ���ϵ�����������ֵΪ4��
��ö��κ���ͼ�������ֵΪ��4��
��2���� ����֪�õ�C������Ϊ��0��c������B������Ϊ��m��0����
���C���������c-0����B���������0-m��
�֡ߵ�B���C�ġ�������ȣ�
��c-0=0-m��
��m=��c��
�� ��m=��c��
��B����c��0����
�������![]() ��
�У�
�ã� ![]() ��
��
��c��0��
��![]() ��
��
��![]() �� ��
�� ��
��![]() �ġ�����Ϊ��
�ġ�����Ϊ��
![]() ��
��
�ߡ�����ֵ��Ϊ1��
��![]() ����
����
���ٴ�����У��ã� ![]()
��![]() ��
��
�������ߵı���ʽΪ![]() ��
��
��3����ͼ������M��ֱ��PF��DE������M�ڵ�P��F��
��ֱ��DE�Ľ���ʽΪ��y=x����M������Ϊ��2��3����
��ֱ��PF�Ľ���ʽΪy=-x+5��
��ֱ��y=x�����е����������0������ֱ��y=x���Ҳ����ֱ��y=xԽԶ�ĵ��������Խ��������M�ϵ�P����ֱ��y=x��Զ��
����P������������M�ġ�����ֵ����
���P��������x��y����
����P����M��2��3���ľ���Ϊ2��
����![]() ��
��
������P��x��y����ֱ��y=-x+5����
��![]() �������
������� ![]() ��
��
����Ӧ���� ![]() ��
��
����P������Ϊ![]() ��
��
����P��������� ![]() ��
��
���M�ġ�����ֵ��Ϊ�� ![]() .
.

 Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�