题目内容
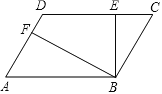
【题目】平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,若CE=2,DF=1,∠EBF=60°,求平行四边形ABCD的面积.
【答案】![]() .
.
【解析】
根据四边形的内角和等于360°,求出∠D=120°,根据平行四边形的性质得到∠A=∠C=60°,进一步求出∠ABF=∠EBC=30°,根据CE=2,DF=1,求出BC、AB的长,根据勾股定理求出BE的长,根据平行四边形的面积公式即可求出答案.
∵BE⊥CD,BF⊥AD,
∴∠BEC=∠BFD=90°,
∵∠EBF=60°,∠D+∠BED+∠BFD+∠EBF=360°,
∴∠D=120°,
∵平行四边形ABCD,
∴DC∥AB,AD∥BC,∠A=∠C,
∴∠A=∠C=180°-120°=60°,
∴∠ABF=∠EBC=30°,
∴AD=BC=2EC=4
在△BEC中由勾股定理得:BE=![]() ,
,
在△ABF中AF=4-1=3,
∵∠ABF=30,
∴AB=6,
∴平行四边形ABCD的面积是ABBE=![]() .
.

练习册系列答案
相关题目