题目内容
【题目】A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.
(1)设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.
(2)若总运费不超过9000元,问有几种调运方案?
(3)求出总运费最低的调运方案,并求出最低运费.
【答案】
(1)解:由题意可得,
w=400(10﹣x)+800(2+x)+300x+500(6﹣x)=200x+8600.
由 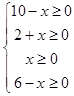 解得0≤x≤6.
解得0≤x≤6.
(2)解:由题意200x+8600≤9000,
解得x≤2,
∴x=0或1或2,
∴有三种调运方案:①B市运往C市的联合收割机为0台,B市运往D市的联合收割机为6台,A市运往C市的联合收割机为10台,A市运往D市的联合收割机为2台;
②B市运往C市的联合收割机为1台,B市运往D市的联合收割机为5台,A市运往C市的联合收割机为9台,A市运往D市的联合收割机为3台;
③B市运往C市的联合收割机为2台,B市运往D市的联合收割机为4台,A市运往C市的联合收割机为8台,A市运往D市的联合收割机为4台;
(3)解:∵w=200x+8600,
∵200>0,
∴w随x的增大而增大,
∵0≤x≤6,
∴x=0时,w最小,最小值为8600元.
【解析】(1)根据题意求出各个运费之和即可,利用不等式组确定自变量的取值范围即可.(2)列出不等式即可解决问题.(3)利用一次函数的增减性即可解决问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目