题目内容
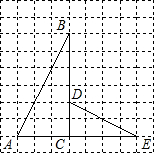
如图，△ABC是等边三角形，D、E在BC所在的直线上，且AB•AC=BD•CE．
求证：△ABD∽△ECA．
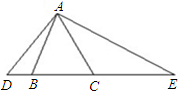
求证：△ABD∽△ECA．
证明：∵△ABC是等边三角形（已知），
∴∠ABC=∠ACB=60°（等边三角形的三内角相等，都等于60°），
∴∠ABD=∠ACE（等角的补角相等），
又AB•AC=BD•CE（已知），即
=
，
∴△ABD∽△ECA（两边对应成比例且夹角相等的两三角形相似）．
∴∠ABC=∠ACB=60°（等边三角形的三内角相等，都等于60°），
∴∠ABD=∠ACE（等角的补角相等），
又AB•AC=BD•CE（已知），即
| AB |
| BD |
| EC |
| CA |
∴△ABD∽△ECA（两边对应成比例且夹角相等的两三角形相似）．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
