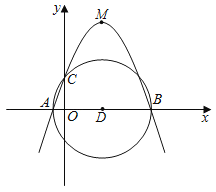题目内容
【题目】已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
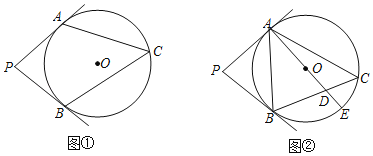
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
【答案】(1)50°;(2)20°
【解析】
(1)连接OA、OB,根据切线的性质得到∠OAP=∠OBP=90°,根据四边形内角和等于360°求出∠AOB的度数,然后根据圆周角定理求解即可;
(2)连接CE,根据圆周角定理得到∠ACE=90°,根据等腰三角形的性质、三角形的外角性质计算即可.
解:(1)连接OA、OB,

∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°﹣90°﹣90°﹣80°=100°,
由圆周角定理得,∠ACB=![]() ∠AOB=50°;
∠AOB=50°;
(2)连接CE,

∵AE为⊙O的直径,
∴∠ACE=90°,
∵∠ACB=50°,
∴∠BCE=90°﹣50°=40°,
∴∠BAE=∠BCE=40°,
∵AB=AD,
∴∠ABD=∠ADB=70°,
∴∠EAC=∠ADB﹣∠ACB=20°.

练习册系列答案
相关题目
【题目】某校九年级学生某科目学期总评成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果学期总评成绩80分以上(含80分),则评定为“优秀”,下表是小张和小王两位同学的成绩记录:
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 | _______ |
若按完成作业、单元检测、期末考试三项成绩按1:2:7的权重来确定学期总评成绩.
(1)请计算小张的学期总评成绩为多少分?
(2)小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?