��Ŀ����
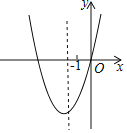
����Ŀ����ͼ��������y����![]() x2+2x+6��x����A��B���㣨��A�ڵ�B���Ҳࣩ����y���ڵ�C������ΪD���Գ���քe��x�ᡢ�߶�AC�ڵ�E��F��
x2+2x+6��x����A��B���㣨��A�ڵ�B���Ҳࣩ����y���ڵ�C������ΪD���Գ���քe��x�ᡢ�߶�AC�ڵ�E��F��
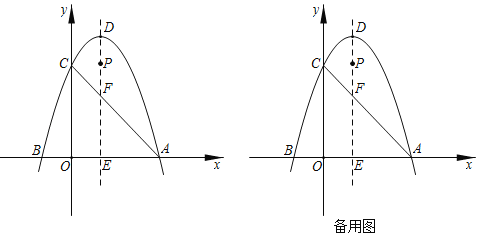
��1���������ߵĶԳ��ἰ��A�����ꣻ
��2������AD��CD������ACD�������
��3���趯��P�ӵ�D���������߶�DE�������յ�E�˶���ȡ��ACDһ�ߵ����˵�͵�P������������Ϊ������������ǵ��������Σ���PΪ���Ƕ��㣬���������������ĵ�P�����꣮
���𰸡���1�������ߵĶԳ���x��2��A��6��0������2����ACD�����Ϊ12����3����P������Ϊ��2��2����2��6����2��3����
��������
��1����y=0�����x�����������A��B�����꣬��x��0�����y���������C�����꣬�ٸ��ݶԳ��ṫʽ������������ߵĶԳ��
��2���Ƚ����κ�����һ��ʽ���ɶ���ʽ�����������D�����꣬���ô���ϵ�������ֱ��AC�Ľ���ʽ���Ӷ������F�����꣬���ݡ�Ǧ���ߣ�ˮƽ������������ɣ�
��3�����ݵ��������εĵ������ۣ��ٹ���O��OM��AC��DE�ڵ�P����AC�ڵ�M�����ݵ��������ε����ʺʹ�ֱƽ���ߵ����ʼ��ɵó���ʱACΪ����������ACP�ĵױߣ��ҡ�OEPΪ����ֱ�������Σ��Ӷ������P���ꣻ�ڹ���C��CP��DE�ڵ�P�����PD���ɵô�ʱ��PCD����CDΪ�ױߵĵ���ֱ�������Σ��Ӷ������P���ꣻ����AD�Ĵ�ֱƽ���߽�DE�ڵ�P�����ݴ�ֱƽ���ߵ����ʿɵ�PD��PA����PD��x�����ݹ��ɶ����г����̼������x���Ӷ������P������.
��1������������y����![]() x2+2x+6��y��0���õ���
x2+2x+6��y��0���õ���![]() x2+2x+6��0�����x����2��6��
x2+2x+6��0�����x����2��6��
��B����2��0����A��6��0����
��x��0���õ�y��6��
��C��0��6����
�������ߵĶԳ���x����![]() ��2��A��6��0����
��2��A��6��0����
��2����y����![]() x2+2x+6��
x2+2x+6��![]() ��
��
�������ߵĶ�������D��2��8����
��ֱ��AC�Ľ���ʽΪy��kx+b��
��A��6��0����C��0��6���������ʽ����
![]()
��ã�![]() ��
��
��ֱ��AC�Ľ���ʽΪy����x+6��
��x=2����y����x+6�����y=4
��F��2��4����
��DF��4��
��![]() ��
��![]() ��12��
��12��
��3������ͼ1������O��OM��AC��DE�ڵ�P����AC�ڵ�M��
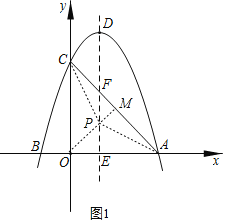
��A��6��0����C��0��6����
��OA��OC��6��
��CM��AM����MOA=![]() ��COA=45��
��COA=45��
��CP��AP����OEPΪ����ֱ�������Σ�
���ʱACΪ����������ACP�ĵױߣ�OE��PE��2��
��P��2��2����
����ͼ2������C��CP��DE�ڵ�P��
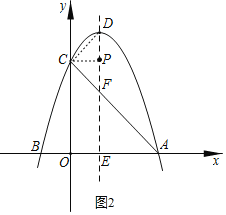
��OC��6��DE��8��
��PD��DE��PE��2��
��PD��PC��
��ʱ��PCD����CDΪ�ױߵĵ���ֱ�������Σ�
��P��2��6����
����ͼ3����AD�Ĵ�ֱƽ���߽�DE�ڵ�P��
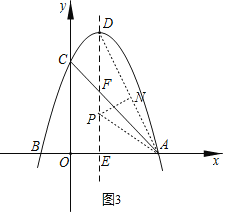
��PD��PA��
��PD��x����PE��8��x����Rt��PAE��PE2+AE2��PA2��
�ࣨ8��x��2+42��x2��
���x��5��
��PE��8��5=3��
��P��2��3����
������������P��������2��2����2��6����2��3����