Question

【题目】如图，在中，点在边上，，连接交于点，则的面积与四边形的面积之比为（ ）

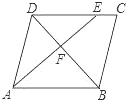
A. 3∶4 B. 9∶16 C. 9∶19 D. 9∶28

Answer 1

【答案】C

【解析】

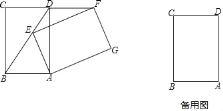
由DE：EC=3：1，可得DF：FB=3：4，根据在高相等的情况下三角形面积比等于底边的比，可得S△EFD：S△BEF=3：4，S△BDE：S△BEC=3：1，可求△DEF的面积与四边形BCEF的面积的比值．

连接BE

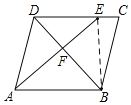
∵DE：EC=3：1

∴设DE=3k，EC=k，则CD=4k

∵ABCD是平行四边形

∴AB∥CD，AB=CD=4k

∴

∴S△EFD：S△BEF=3：4

∵DE：EC=3：1

∴S△BDE：S△BEC=3：1

设S△BDE=3a，S△BEC=a

则S△EFD=，S△BEF=

∴SBCEF=S△BEC+S△BEF=

∴则△DEF的面积与四边形BCEF的面积之比9：19

故选C．