Question

【题目】将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．

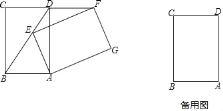
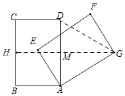
（1）如图，当点E在BD上时．求证：FD＝CD；

（2）当α为何值时，GC＝GB？画出图形，并说明理由．

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】

（1）先运用SAS判定△AED≌△FDE，可得DF=AE，再根据AE=AB=CD，即可得出CD=DF；

（2）当GB=GC时，点G在BC的垂直平分线上，分两种情况讨论，依据∠DAG=60°，即可得到旋转角α的度数．

（1）由旋转可得，AE＝AB，∠AEF＝∠ABC＝∠DAB＝90°，EF＝BC＝AD，

∴∠AEB＝∠ABE，

又∵∠ABE+∠EDA＝90°＝∠AEB+∠DEF，

∴∠EDA＝∠DEF，

又∵DE＝ED，

∴△AED≌△FDE（SAS），

∴DF＝AE，

又∵AE＝AB＝CD，

∴CD＝DF；

（2）如图，当GB＝GC时，点G在BC的垂直平分线上，

分两种情况讨论：

①当点G在AD右侧时，取BC的中点H，连接GH交AD于M，

∵GC＝GB，

∴GH⊥BC，

∴四边形ABHM是矩形，

∴AM＝BH＝AD＝AG，

∴GM垂直平分AD，

∴GD＝GA＝DA，

∴△ADG是等边三角形，

∴∠DAG＝60°，

∴旋转角α＝60°；

②当点G在AD左侧时，同理可得△ADG是等边三角形，

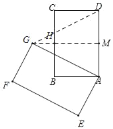
∴∠DAG＝60°，

∴旋转角α＝360°﹣60°＝300°．