题目内容
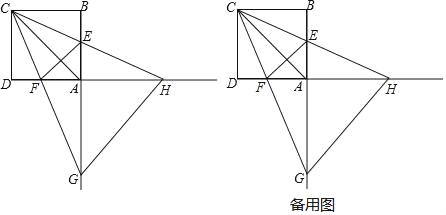
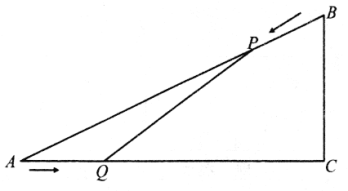
【题目】如图,已知![]() 中,
中,![]() cm,
cm,![]() cm,
cm,![]() cm.点
cm.点![]() 由
由![]() 出发,以5cm/s的速度沿
出发,以5cm/s的速度沿![]() 向点
向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由
由![]() 出发,以4cm/s的速度沿
出发,以4cm/s的速度沿![]() 向点
向点![]() 匀速运动.连接
匀速运动.连接![]() ,设运动时间为
,设运动时间为![]() (单位:
(单位:![]() ,
,![]() ).
).
(1)求点![]() 到
到![]() 的距离(用含
的距离(用含![]() 代数式表示);
代数式表示);
(2)求![]() 为何值时,线段
为何值时,线段![]() 将
将![]() 的面积分成的两部分的面积比为3∶13;
的面积分成的两部分的面积比为3∶13;
(3)当![]() 为直角三角形时,求
为直角三角形时,求![]() 的值.
的值.
【答案】(1)![]() (2)1或3 (3)2或
(2)1或3 (3)2或![]()
【解析】
(1)先判断出△ABC是直角三角形,进而求出∠A的正弦值,再表示出AP,即可得出结论;
(2)先求出△ABC的面积,进而得出△APQ=78或18建立方程求解即可;
(3)分两种情况,利用相似三角形得出比例式建立方程求解即可得出结论.
(1)在△ABC中,AB=20cm,AC=16cm,BC=12cm,
∴AC2+BC2=162+122=400=202=AB2,
∴△ABC是直角三角形,
∴sinA=![]() ,
,
由运动知,BP=5t,
∴AP=20-5t,
过点P作PD⊥AC于D,
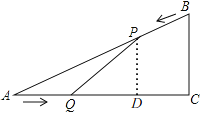
在Rt△APD中,sinA=![]() ,
,
∴DP=3(4-t),
∴点P到AC的距离为3(4-t);
(2)由运动知AQ=4t,
由(1)知,DP=3(4-t),
∴S△APQ=![]() AQDP=6t(4-t),
AQDP=6t(4-t),
∵AC=16,BC=12,
∴S△ABC=![]() ACBC=96,
ACBC=96,
∵线段PQ将△ABC的面积分成的两部分的面积之比为3:13,
∴S△APQ=![]() S△ABC=18或S△APQ=
S△ABC=18或S△APQ=![]() S△ABC=78,
S△ABC=78,
∴6t(4-t)=18或6t(4-t)=78,
当6t(4-t)=18时,t=1秒或3秒
当6t(4-t)=78时,此方程无实数根,
即:t=1秒或3秒时,线段PQ将△ABC的面积分成的两部分的面积之比为3:13;
(3)当△APQ为直角三角形时,
①∠APQ=90°=∠ACB,
∵∠A=∠A,
∴△APQ∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴t=![]() 秒,
秒,
②当∠AQP=90°=∠ACB,
∵∠A=∠A,
∴△AQP∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴t=2秒,
即:当△APQ为直角三角形时,t=2秒或![]() 秒.
秒.

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.