题目内容
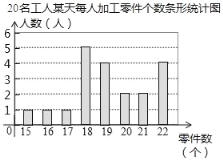
【题目】某部门为了解工人的生产能力情况,进行了抽样调查.该部门随机抽取了20名工人某天每人加工零件的个数,数据如下:整理上面数据,得到条形统计图;样本数据的平均数、众数、中位数如表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 19.2 | m | n |
根据以上信息,解答下列问题:
(1)上表中m、n的值分别为 , ;
(2)为调动积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让60%左右的工人能获奖,应根据 来确定奖励标准比较合适(填“平均数”、“众数”或“中位数”);
(3)该部门规定:每天加工零件的个数达到或超过21个的工人为生产能手若该部门有300名工人,试估计该部门生产能手的人数;
(4)现决定从小王、小张、小李、小刘中选两人参加业务能手比赛,直接写出恰好选中小张、小李两人的概率.
【答案】(1)18,19;(2)中位数;(3)90(人);(4)![]()
【解析】
(1)根据条形统计图中的数据,结合众数和中位数的概念可以得到m、n的值;
(2)根据题意可知应选择中位数比较合适;
(3)根据统计图中的数据可以计该部门生产能手的人数.
(4)根据题意先画出树状图,得出所有等可能性的结果,再根据概率公式即可得出答案.
(1)由条形图知,数据18出现的次数最多,
所以众数m=18;
中位数是第10、11个数据的平均数,而第10、11个数据都是19,
所以中位数n=![]() =19,
=19,
故答案为:18,19;
(2)由题意可得,如果想让60%左右的工人能获奖,应根据中位数来确定奖励标准比较合适,
故答案为:中位数;
(3)若该部门有300名工人,估计该部门生产能手的人数为300×![]() =90(人);
=90(人);
(4)将小王、小张、小李、小刘分别记为甲、乙、丙、丁,
画树状图如下:
![]()
∵共有12种等可能性的结果,恰好选中乙、丙两位同学的有2种,
∴恰好选中小张、小李两人的概率为![]() .
.